
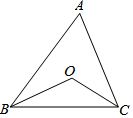
 如图,△ABC中,∠A=70°,BO平分∠ABC,CO平分∠ACB,求∠BOC的度数.
如图,△ABC中,∠A=70°,BO平分∠ABC,CO平分∠ACB,求∠BOC的度数.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
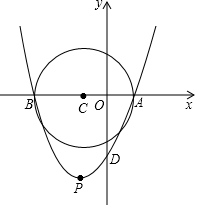 如图,已知⊙C的圆心在x轴上,且进过A(1,0),B(-3,0)两点,抛物线y=ax2+bx+c(a>0)经过A、B两点,顶点为P.
如图,已知⊙C的圆心在x轴上,且进过A(1,0),B(-3,0)两点,抛物线y=ax2+bx+c(a>0)经过A、B两点,顶点为P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
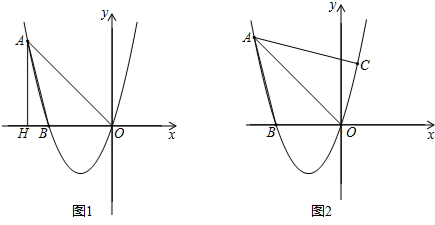
 如图,两个村庄A、B在河CD的同侧,A、B两村到河的距离分别为AC=1千米,BD=3千米,CD=3千米.现要在河边CD上建造一水厂,向A、B两村送自来水.铺设水管的工程费用为每千米20000元,请你在CD上选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用W.
如图,两个村庄A、B在河CD的同侧,A、B两村到河的距离分别为AC=1千米,BD=3千米,CD=3千米.现要在河边CD上建造一水厂,向A、B两村送自来水.铺设水管的工程费用为每千米20000元,请你在CD上选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用W.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com