
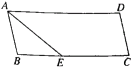
【题目】如图,ABCD中,点E是CD延长线上一点,BE交AD于点F,DE=![]() CD.
CD.
(1)求证:△ABF∽△CEB
(2)若△DEF的面积为2,求ABCD的面积.
(3)若G、H分别为BF、AB的中点,AG、FH交于点O,求![]() .
.

【答案】(1)证明见解析;(2)24;(3)1:2.
【解析】
(1)由ABCD可知AB∥CD且∠BAD=∠C,据此可进行证明;
(2)先证明△DFD分别与△BAF、△EBC相似,利用相似比分别求出S△BFA和S梯形FDBC的面积;
(3)由G、H分别为BF、AB的中点可知GH为中位线,进而可证明△OHG∽△OAF并进行求解.
(1)证明:∵ABCD,
∴AB∥CE,AD∥BC,
∴∠ABF=∠E,
又∵ABCD是平行四边形,
∴∠BAF=∠C,
△ABF∽△CEB,
(2)解:∵∠ABF=∠E,∠AFB=∠EFD,
∴△ABF∽△DEF,
∵AD∥BC,
∴△CEB∽△DEF,
∵DE=![]() CD,
CD,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵△DEF的面积为2,
∴S△BFA=8,S△EBC=18,
∴S梯形FDBC=18﹣2=16,
∴S平行四边形ABCD=16+8=24,
(3)解:∵G、H为中点,
∴GH∥AF,2GH=AF,
∴OG:OA=HG:AF=1:2.


科目:初中数学 来源: 题型:
【题目】某商场计划销售甲、乙两种产品共![]() 件,每销售
件,每销售![]() 件甲产品可获得利润
件甲产品可获得利润![]() 万元, 每销售
万元, 每销售![]() 件乙产品可获得利润
件乙产品可获得利润![]() 万元,设该商场销售了甲产品
万元,设该商场销售了甲产品![]() (件),销售甲、乙两种产品获得的总利润为
(件),销售甲、乙两种产品获得的总利润为![]() (万元).
(万元).
(1)求![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)若每件甲产品成本为![]() 万元,每件乙产品成本为
万元,每件乙产品成本为![]() 万元,受商场资金影响,该商场能提供的进货资金至多为
万元,受商场资金影响,该商场能提供的进货资金至多为![]() 万元,求出该商场销售甲、乙两种产品各为多少件时,能获得最大利润.
万元,求出该商场销售甲、乙两种产品各为多少件时,能获得最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.

(1)求直线![]() 与坐标轴围成的面积;
与坐标轴围成的面积;
(2)在![]() 轴上一动点
轴上一动点![]() ,使
,使![]() 是等腰三角形;请直接写出所有
是等腰三角形;请直接写出所有![]() 点的坐标,并求出如图所示
点的坐标,并求出如图所示![]() 时点
时点![]() 的坐标;
的坐标;
(3)直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ;点
;点![]() 是直线
是直线![]() 上一点,若
上一点,若![]() 的面积是
的面积是![]() 的面积的两倍,求点
的面积的两倍,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 一内角的平分线与边相交并把这条边分成2cm,3cm的两条线段,求
一内角的平分线与边相交并把这条边分成2cm,3cm的两条线段,求![]() 的周长.
的周长.
小华的解答过程如下:
如图,![]() 平分
平分![]() 一内角
一内角![]() .
.
当![]() 时,∵
时,∵![]() 平分
平分![]() ,
,
∴![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() .∴
.∴![]() 的周长为
的周长为![]() .
.
你认为小华的解答过程对吗?如果不对,请写出正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是![]() 的的直径,BC
的的直径,BC![]() AB于点B,连接OC交
AB于点B,连接OC交![]() 于点E,弦AD//OC,弦DF
于点E,弦AD//OC,弦DF![]() AB于点G.
AB于点G.
(1)求证:点E是![]() 的中点;
的中点;
(2)求证:CD是![]() 的切线;
的切线;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一水池中有水![]() ,如果每分钟放出
,如果每分钟放出![]() 的水,水池里的水量与放水时间有如下关系:
的水,水池里的水量与放水时间有如下关系:
放水时间(分) | 1 | 2 | 3 | 4 | … |
水池中水量 | 38 | 36 | 34 | 32 | … |
下列数据中满足此表格的是( )
A.放水时间8分钟,水池中水量![]() B.放水时间20分钟,水池中水量
B.放水时间20分钟,水池中水量![]()
C.放水时间26分钟,水池中水量![]() D.放水时间18分钟,水池中水量
D.放水时间18分钟,水池中水量![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com