
 .
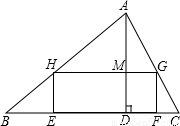
.
 ,
,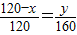
 x+160(或x=-
x+160(或x=- y+120);
y+120); x2+160x=-
x2+160x=- (x2-120x)=-
(x2-120x)=- (x2-120x+3600-3600)
(x2-120x+3600-3600) (x-60)2+4800.
(x-60)2+4800. ×60+160=80cm.
×60+160=80cm.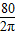 cm,铁桶体积V1=π•(
cm,铁桶体积V1=π•(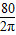 )2•60=
)2•60=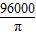 cm3.
cm3. cm,铁桶体积V2=π•(
cm,铁桶体积V2=π•( )2•80=
)2•80=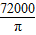 cm3.
cm3.

科目:初中数学 来源:2004年全国中考数学试题汇编《三角形》(04)(解析版) 题型:填空题
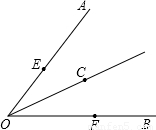
查看答案和解析>>
科目:初中数学 来源:2010年浙江省温州市洞头县中考数学一模试卷(解析版) 题型:选择题
 的中点,那么∠DAC的度数是( )
的中点,那么∠DAC的度数是( )
查看答案和解析>>
科目:初中数学 来源:2009年浙江省嘉兴市数学素质评估卷4(秀洲区王江泾镇实验学校)(解析版) 题型:选择题

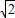
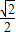
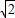
查看答案和解析>>
科目:初中数学 来源:2004年四川省中考数学试卷(课标卷)(解析版) 题型:填空题
 于点D,连接OA、OB、AP、BP.根据以上条件,写出三个正确结论(OA=OB除外):① ;② ;③ .
于点D,连接OA、OB、AP、BP.根据以上条件,写出三个正确结论(OA=OB除外):① ;② ;③ .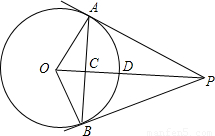
查看答案和解析>>
科目:初中数学 来源:2004年四川省中考数学试卷(解析版) 题型:选择题
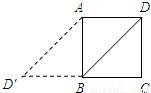

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com