
����Ŀ��������ͼ�ν�����������Ӧ��ʮ�ֹ㷺���ر�����Щ�����Ժ�ǿ����Ŀ��������ܷ�����Ŀ���������ļ������壬����ͨ���Ĵ�������ȥ˼�������������������룬�������֣���ʱ�������ת��˼ά��������Ŀ�������ļ���������ͨ�������ʺϵļ���ͼ�Σ�����õ��°빦����Ч���������������ʵ����
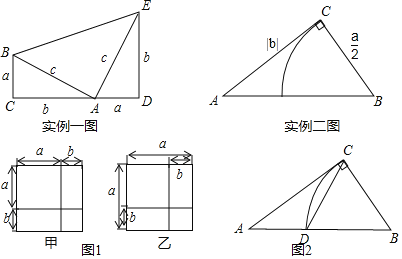
ʵ��һ��1876�꣬������ͳ٤�Ƕ�������ʵ��һͼ֤���˹��ɶ�������S�ı���ABCD=S��ABC+S��ADE+S��ABE�ã�![]() ��a+b��2=2��
��a+b��2=2��![]() ab+
ab+![]() c2������ã�a2+b2=c2��
c2������ã�a2+b2=c2��
ʵ������ŷ����õġ�����ԭ�������أ�����x�ķ���x2+ax=b2��ͼ�ⷨ�ǣ���Rt��ABC��ʹ��ACB=90����BC=![]() ��AC=|b|������б��AB�Ͻ�ȡBD=
��AC=|b|������б��AB�Ͻ�ȡBD=![]() ����AD�ij����Ǹ÷��̵�һ����������ʵ����ͼ����
����AD�ij����Ǹ÷��̵�һ����������ʵ����ͼ����
����������Ķ����ϻش���������⣺
��1����ͼ1��������ͼ��������ĵ�����ϵ��д����ͼҪ֤������ѧ��ʽ��______����ͼҪ֤������ѧ��ʽ��______�����ֵ���ѧ˼����______��
��2����ͼ2����2��-8�ǹ���x�ķ���x2+ax=b2��������������ʵ�����ķ�ʽ����Rt��ABC������CD����CD�ij���
��3����x��y��z��Ϊ��������x2+y2=z2�����ù���ͼ�εķ�����![]() �����ֵ��
�����ֵ��
���𰸡���1����ȫƽ����ʽ��ƽ���ʽ�����ν�ϵ�˼�루2��![]() ��3��
��3��![]()
��������
��1�����������������⼴�ɣ�
��2����ͼ2�У���CH��AB��H�������⣬AD=2��BC=BD=3��AC=4��������������CH��BH��DH���ɽ�����⣻
��3����ͼ3�У���4��ȫ�ȵ�ֱ�������Σ�ֱ�DZ߷ֱ�Ϊx��y��б��Ϊz����ƴ��ͼ�����Σ���x+y�Ƕ�ֵʱ��z��С��ʱ��![]() ��ֵ��С����֪��С�����εĶ����Ǵ������ε��е�ʱ��z��ֵ��С����ʱx=y��z=
��ֵ��С����֪��С�����εĶ����Ǵ������ε��е�ʱ��z��ֵ��С����ʱx=y��z=![]() x���ɴ˼��ɽ�����⣮
x���ɴ˼��ɽ�����⣮
��1����ͼ1�У�ͼ�״������ε����=��a+b��2=a2+2ab+b2��
ͼ���д������ε����=a2=��a-b��2+b2+2b��a-b����
��a2-b2=��a-b����a-b+2b��=��a+b����a-b����
��ͼҪ֤������ѧ��ʽ����ȫƽ����ʽ����ͼҪ֤������ѧ��ʽ��ƽ���ʽ�����ֵ���ѧ˼�������ν�ϵ�˼�룮
�ʴ�Ϊ����ȫƽ����ʽ��ƽ���ʽ�����ν�ϵ�˼�룮
��2����ͼ2�У���CH��AB��H��
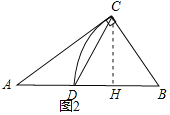
�����⣬AD=2��BC=BD=3��AC=4��
��![]() ACBC=
ACBC=![]() ABCH��
ABCH��
��CH=![]() ��
��
��BH=![]() ��
��
��DH=BD-BH=![]() ��
��
��CD=![]() ��
��
��3����ͼ3�У���4��ȫ�ȵ�ֱ�������Σ�ֱ�DZ߷ֱ�Ϊx��y��б��Ϊz����ƴ��ͼ�����Σ�
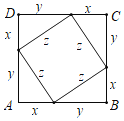
��x+y�Ƕ�ֵʱ��z��С��ʱ��![]() ��ֵ��С��
��ֵ��С��
��֪��С�����εĶ����Ǵ������ε��е�ʱ��z��ֵ��С����ʱx=y��z=![]() x��
x��
��![]() ���ֵ=
���ֵ=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ˮ���е�ţ���ͽ��ӵ�ά���غ����ܸߣ������������ϲ������ũ�����ˮ���̼�11�·ݹ����˵�һ��ţ���ͽ��ӹ�300ǧ�ˣ���֪ţ������ÿǧ��15Ԫ���ۼ�ÿǧ��30Ԫ�����ӽ���ÿǧ��5Ԫ���ۼ�ÿǧ��10Ԫ��
(1)������ţ���ͽ���ȫ�����������������3500Ԫ����ţ�����ٹ�������ǧ�ˣ�
(2)��һ��ţ���ͽ��Ӻܿ����꣬�����̼Ҿ��������ڶ���ţ���ͽ��ӣ�ţ���ͽ��ӵĽ��۲��䣬ţ���ۼ۱ȵ�һ������a%(����aΪ������)�������ۼ۱ȵ�һ������2a%��������(1)�л���������ʱ��������ȣ�ţ���������½�a%�����ӵ��������ֲ��䣬����ڶ������Ѿ�������ţ���ͽ��ӵ������ܶ��(1)�е�һ��ţ���ͽ�����������Ӧ��������ܶ�������2%����������a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
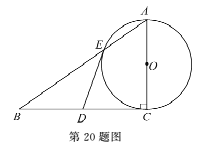
����Ŀ����ͼ����֪Rt��ABC,��C=90�㣬DΪBC���е�.��ACΪֱ����ԲO��AB�ڵ�E.
��1����֤��DE��ԲO������.
(2)��AE:EB=1:2,BC=6����AE�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
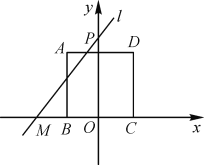
����Ŀ����ͼ��������ABCD�ı߳�Ϊ2��BC����x���ϣ�BC���е���ԭ��O�غϣ�������M(��2��0)�붯��P(0��t)��ֱ��MP����l.
(1)��l�Ľ���ʽΪy��2x��4���жϴ�ʱ��A�Ƿ���ֱ��l�ϣ���˵�����ɣ�
(2)��ֱ��l��AD���й�����ʱ����t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ɲ�����������һ���ֿ�����ͬ�����Ĺ��˺ͻ����ˣ���Ϊx��������x��5����ƽʱÿ�춼ֻ����8Сʱ��ÿ��������ÿСʱ�ӹ��������֡��𡢰�װһ�廯����������ÿ������ÿСʱ�ӹ�����������2�����������������ٽ����˹���ȱ��������İ������࣬��˾����������2�������ˣ��ҽ�������ÿ�칤��ʱ���ӳ���12Сʱ������ÿ�������˽����������죬������ÿ��������ÿСʱ�ӹ�������������ԭ�л���������x��������������л�����ÿ��ӹ����������������й���ƽʱÿ��ӹ�����������6������òֿ�ƽʱһ��ӹ�______��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��y����![]() x�뷴��������y��
x�뷴��������y��![]() ��ͼ����A��B���㣨��A�ڵ�B��ࣩ����֪A�����������2��
��ͼ����A��B���㣨��A�ڵ�B��ࣩ����֪A�����������2��
��1�����������ı���ʽ��
��2������ͼ��ֱ��д����![]() x��
x��![]() �Ľ⼯��
�Ľ⼯��
��3����ֱ��l1��y��- ![]() x��y����ƽ�ƺ��ֱ��l2�뷴��������y��
x��y����ƽ�ƺ��ֱ��l2�뷴��������y��![]() �ڵڶ������ڽ��ڵ�C�������ABC�����Ϊ30����ƽ�ƺ��ֱ��l2�ĺ�������ʽ��
�ڵڶ������ڽ��ڵ�C�������ABC�����Ϊ30����ƽ�ƺ��ֱ��l2�ĺ�������ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��P��B��C��Բ�ϵ��ĸ��㣬��APC=��CPB=60�㣬AP��CB���ӳ����ཻ�ڵ�D��
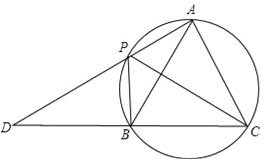
��1����֤����ABC�ǵȱ������Σ�
��2������PAC=90�㣬AB=![]() ����PD�ij���
����PD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������ABC�У���D��E�ֱ��ڱ�AC��AB�ϣ�AG��BC�ڵ�G��AF��DE�ڵ�F����EAF=��GAC��
��1����֤����ADE�ס�ABC��
��2����AD=3��AB=5����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ҹ��������ķ�չ��������������������Խ��Խ�ߣ�ij����Ϊ���˽��ͥ�����Ļ���������������������ȡ���ּ�ͥ����ÿ����ͥ���Ļ����������ѽ������ʾ����飬���ݵ��������Ƴ�����������������ͳ��ͼ����
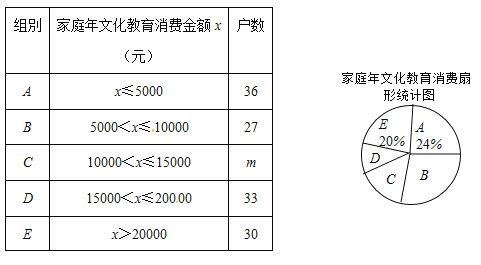
�������ͳ��ͼ���ṩ����Ϣ������������⣺
��1�����α�����ļ�ͥ��������������m=������
��2����˵�����ε������ݵ���λ��������һ�飿
��3��������ͳ��ͼ�У�D���������ε�Բ�Ľ�Ϊ���ٶȣ�
��4�����������2500����ͥ������������Ļ�����������10000Ԫ���ϵļ�ͥ�ж��ٻ���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com