
 如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°. 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
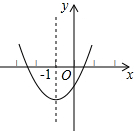 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①abc<0;②2a+b=0;③a+b+c>0;④b2>4ac.其中正确的有①③④.
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①abc<0;②2a+b=0;③a+b+c>0;④b2>4ac.其中正确的有①③④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC在第一象限,其面积为8.点P从点A出发,沿△ABC的边从A-B-C-A运动一周,在点P运动的同时,作点P关于原点O的对称点Q,再以PQ为边作等边三角形PQM,点M在第二象限,点M随点P运动所形成的图形的面积为24.
如图,△ABC在第一象限,其面积为8.点P从点A出发,沿△ABC的边从A-B-C-A运动一周,在点P运动的同时,作点P关于原点O的对称点Q,再以PQ为边作等边三角形PQM,点M在第二象限,点M随点P运动所形成的图形的面积为24.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com