
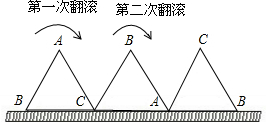
 一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,若翻滚了2017次,则B点所经过的路径长度为$\frac{2690}{3}$π.
一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,若翻滚了2017次,则B点所经过的路径长度为$\frac{2690}{3}$π. 分析 B点翻滚一周所走过的路径长度为两段弧长,一段是以点C为圆心,BC为半径,圆心角为120°,第二段是以A为圆心,AB为半径,圆心角为120°的两段弧长,依弧长公式计算即可.
解答 解:从图中发现:B点从开始至结束所走过的路径长度为两段弧长
即第一段=$\frac{120×1}{180}$,第二段=$\frac{120π×1}{180}$.
故B点翻滚一周所走过的路径长度=$\frac{120π×1}{180}$+$\frac{120π×1}{180}$=$\frac{4π}{3}$,
∵2017÷3=672…1,
∴若翻滚了2017次,则B点所经过的路径长度=672×$\frac{4π}{3}$+$\frac{120π×1}{180}$=$\frac{2690}{3}$π,
故答案为:$\frac{2690}{3}$π.
点评 本题考查了旋转的性质,等边三角形的性质,扇形面积的计算,求出两次旋转的角度是解题的关键.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:解答题
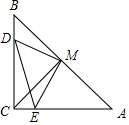 如图,在Rt△ABC中,∠ACB=90°,BC=AC,D、E分别在BC、AC上,且BD=CE,M是AB的中点,连接DM、ME、DE、CM,△MDE是等腰三角形吗?请说明理由.
如图,在Rt△ABC中,∠ACB=90°,BC=AC,D、E分别在BC、AC上,且BD=CE,M是AB的中点,连接DM、ME、DE、CM,△MDE是等腰三角形吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
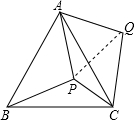 P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC=3:4:2.
P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC=3:4:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为α、b、c,且α=20,∠B=35°,解这个三角形.(精确到0.1,参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为α、b、c,且α=20,∠B=35°,解这个三角形.(精确到0.1,参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形RFGD的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,且DE=2EF,△ABC中,边BC的长度为12cm,高AH为8cm,求矩形DEFG的面积.
如图,矩形RFGD的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,且DE=2EF,△ABC中,边BC的长度为12cm,高AH为8cm,求矩形DEFG的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com