
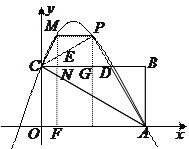
(本题满分9分)已知如图,矩形 的长
的长 ,宽
,宽 ,将
,将 沿
沿 翻折得
翻折得 .
.
(1)填空: 度,
度, 点坐标为( , );
点坐标为( , );
(2)若 两点在抛物线
两点在抛物线 上,求
上,求 的值,并说明点
的值,并说明点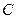 在此抛物线上;
在此抛物线上;
(3)在(2)中的抛物线 段(不包括
段(不包括 点)上,是否存在一点
点)上,是否存在一点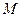 ,使得四边形
,使得四边形 的面积最大?若存在,求出这个最大值及此时
的面积最大?若存在,求出这个最大值及此时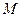 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
解:(1)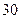 ,
,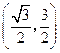 ················································ 4分
················································ 4分
(2)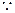 点
点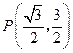 ,
,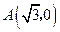 在抛物线上,
在抛物线上,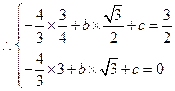 ······················································ 2分
······················································ 2分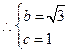
 抛物线的解析式为
抛物线的解析式为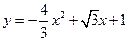 ······································ 1分
······································ 1分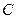 点坐标为
点坐标为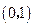
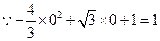
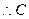 点在此抛物线上. ····························································· 1分
点在此抛物线上. ····························································· 1分
(3)假设存在这样的点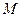 ,使得四边形
,使得四边形 的面积最大.
的面积最大.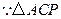 面积为定值,
面积为定值, 要使四边形
要使四边形 的面积最大,只需使
的面积最大,只需使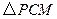 的面积最大.
的面积最大.
过点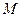 作
作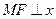 轴分别交
轴分别交 和
和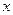 轴于
轴于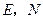 和
和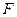 ,过点
,过点 作
作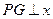 轴交
轴交 于
于 .
.
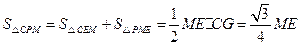
设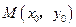 ,
,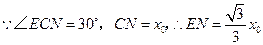
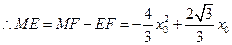
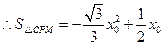 ························································ 2分
························································ 2分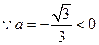 ,
,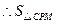 有最大值.
有最大值.
当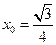 时,
时,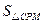 的最大值是
的最大值是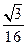 ,
,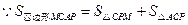
 四边形
四边形 的面积的最大值为
的面积的最大值为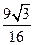 . ··································· 1分
. ··································· 1分
此时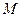 点的坐标为
点的坐标为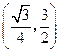 . ·················································· 1分
. ·················································· 1分
所以存在这样的点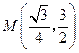 ,使得四边形
,使得四边形 的面积最大,其最大值为
的面积最大,其最大值为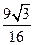 .
.
解析


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年上海市闸北区中考一模数学试卷(解析版) 题型:解答题
(本题满分10分)
已知:如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点M、N分别在边AO和边OD上,且AM= AO,ON=
AO,ON= OD,设
OD,设 =
= ,
, =
= ,试用
,试用 、
、 的线性组合表示向量
的线性组合表示向量 和向量
和向量 .
.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年上海市闸北区中考一模数学试卷(解析版) 题型:解答题
(本题满分10分)
已知:如图六,九年级某班同学要测量校园内旗杆CH的高度,在地面的点E处用测角器测得旗杆顶点C的仰角∠CAD=45°,再沿直线EF向着旗杆方向行走10米到点F处,在点F又用测角器测得旗杆顶点C的仰角∠CBA=60°;已知测角器的高度为1.6米,求旗杆CH的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省盐城地区九年级上学期期末考试数学卷 题型:解答题
(本题满分10分)
已知二次函数
1.(1)怎样平移这个函数的图象,才能使它经过 和
和 两点?写出平移后的新函数的解析式;
两点?写出平移后的新函数的解析式;
2. (2) 求使新函数的图象位于 轴上方的实数
轴上方的实数 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com