
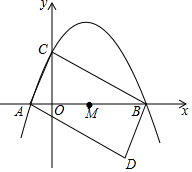
 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A,B,与y轴交于点C.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A,B,与y轴交于点C.分析 (1)直接利用y=0,x=0分别得出A,B,C的坐标;
(2)①利用旋转的性质结合三角形各边长得出D点坐标;
②利用平行四边形的判定方法结合勾股定理的逆定理得出四边形ADBC的形状;
(3)直接利用相似三角形的判定与性质结合三角形各边长进而得出答案.
解答 解:(1)当y=0时,0=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2,
解得:x1=-1,x2=4,
则A(-1,0),B(4,0),
当x=0时,y=2,
故C(0,2);
(2)①过点D作DE⊥x轴于点E,
∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴DE=2,AO=BE=1,OM=ME=1.5,
∴D(3,-2);
②∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴AC=BD,AD=BC,
∴四边形ADBC是平行四边形,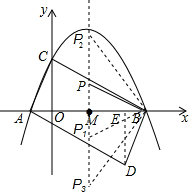
∵AC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
AB=5,
∴AC2+BC2=AB2,
∴△ACB是直角三角形,
∴∠ACB=90°,
∴四边形ADBC是矩形;
(3)由题意可得:BD=$\sqrt{5}$,AD=2$\sqrt{5}$,
则$\frac{BD}{AD}$=$\frac{1}{2}$,
当△BMP∽△ADB时,
$\frac{PM}{BM}$=$\frac{BD}{AD}$=$\frac{1}{2}$,
可得:BM=2.5,
则PM=1.25,
故P(1.5,1.25),
当△BMP1∽△ABD时,
P1(1.5,-1.25),
当△BMP2∽△BDA时,
可得:P2(1.5,5),
当△BMP3∽△BDA时,
可得:P3(1.5,-5),
综上所述:点P的坐标为:(1.5,1.25),(1.5,-1.25),(1.5,5),(1.5,-5).
点评 此题主要考查了二次函数的综合以及相似三角形的判定与性质等知识,正确分类讨论是解题关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
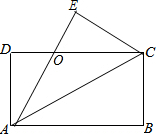 如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )
如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )| A. | 6cm | B. | 7cm | C. | 8cm | D. | 9cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
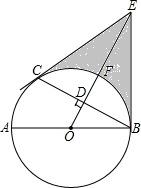 如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
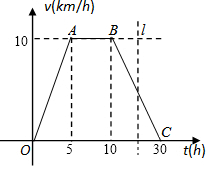 据环保中心观察和预测:发生于甲地的河流污染一直向下游方向移动,其移动速度v(千米/小时)与时间t(小时)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(小时)内污染所经过的路程S(千米).
据环保中心观察和预测:发生于甲地的河流污染一直向下游方向移动,其移动速度v(千米/小时)与时间t(小时)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(小时)内污染所经过的路程S(千米).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com