设点A的坐标为(x,y),其中横坐标x可取-1、2,纵坐标y可取-1、1、2.
(1)求出点A的坐标的所有等可能结果(用树状图或列表法求解);
(2)试求点A与点B(1,-1)关于原点对称的概率.
分析:列举出所有情况,让所求的情况数除以总情况数即为所求的概率.
解答:解:(解法一)
(1)列举所有等可能结果,画出树状图如下

由上图可知,点A的坐标的所有等可能结果为:(-1,-1)、(-1,1)、(-1,2)、
(2,-1)、(2,1)、(2,2),共有6种,(4分)
(2)由(1)知,能与点B(1,-1)关于原点对称的结果有1种.
∴P(点A与点B关于原点对称)=
(4分)
(解法二)(1)列表如下
|
-1 |
1 |
2 |
| -1 |
(-1,-1) |
(-1,1) |
(-1,2) |
| 2 |
(2,-1) |
(2,1) |
(21,2) |
由一表可知,点A的坐标的所有等可能结果为:(-1,-1)、(-1,1)、(-1,2)、
(2,-1)、(2,1)、(2,2),共有6种,(4分)
(2)由(1)知,能与点B(1,-1)关于原点对称的结果有1种.
∴P(点A与点B关于原点对称)=
.(4分)
点评:用到的知识点为:概率=所求情况数与总情况数之比.两点关于原点对称,横纵坐标均互为相反数.





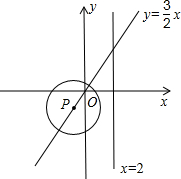 如图,P为正比例函数y=
如图,P为正比例函数y=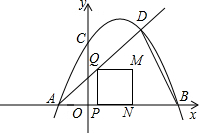 (2012•景宁县模拟)已知二次函数y=-x2+4x+5图象交x轴于点A、B,交y轴于点C,点D是该函数图象上一点,且点D的横坐标为4,连BD,点P是AB上一动点(不与点A重合),过P作PQ⊥AB交射线AD于点Q,以PQ为一边在PQ的右侧作正方形PQMN.设点P的坐标为(t,0).
(2012•景宁县模拟)已知二次函数y=-x2+4x+5图象交x轴于点A、B,交y轴于点C,点D是该函数图象上一点,且点D的横坐标为4,连BD,点P是AB上一动点(不与点A重合),过P作PQ⊥AB交射线AD于点Q,以PQ为一边在PQ的右侧作正方形PQMN.设点P的坐标为(t,0).