
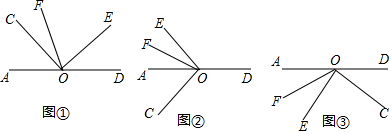
分析 (1)根据已知条件和图形可知:∠COE=90°,∠COE+∠AOC+∠DOE=180°,从而可以得到∠AOC与∠DOE的数量关系;由射线OF平分∠AOE,∠AOC与∠DOE的数量关系,从而可以得到∠COF和∠DOE的数量关系;
(2)由图②,可以得到各个角之间的关系,从而可以得到∠COF和∠DOE之间的数量关系;
(3)由图③和已知条件可以建立各个角之间的关系,从而可以得到∠COF和∠DOE之间的数量关系.
解答 解:(1)∵∠COE=90°,∠COE+∠AOC+∠DOE=180°,
∴∠AOC+∠DOE=90°,
∵射线OF平分∠AOE,
∴∠AOF=∠EOF=$\frac{1}{2}$∠AOE,
∴∠COF=∠AOF-∠AOC=$\frac{1}{2}$∠AOE-(90°-∠DOE)=$\frac{1}{2}$(180°-∠DOE)-90°+∠DOE=$\frac{1}{2}$∠DOE,
故答案为:互余,∠COF=$\frac{1}{2}$∠DOE;
(2)∠COF=$\frac{1}{2}$∠DOE;理由如下:
∵OF平分∠AOE,
∴∠AOF=$\frac{1}{2}$∠AOE,
∵∠COE=90°,
∴∠AOC=90°-∠AOE,
∴∠COF=∠AOC+∠AOF=90°-∠AOE+$\frac{1}{2}$∠AOE=90°-$\frac{1}{2}$∠AOE,
∵∠AOE=180°-∠DOE,
∴∠COF=90°-$\frac{1}{2}$(180°-∠DOE)=$\frac{1}{2}$∠DOE,
即∠COF=$\frac{1}{2}$∠DOE;
(3)∠COF=180°-$\frac{1}{2}$∠DOE;理由如下:
∵OF平分∠AOE,
∴∠EOF=$\frac{1}{2}$∠AOE,
∴∠COF=∠COE+∠EOF=90°+$\frac{1}{2}$∠AOE=90°+$\frac{1}{2}$(180°-∠DOE)=180°-$\frac{1}{2}$∠DOE,
即∠COF=180°-$\frac{1}{2}$∠DOE.
点评 本题考查了角平分线的定义以及角的计算,解题的关键是找出各个角之间的关系,利用数形结合的思想找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
| 造型花卉 | 甲 | 乙 |
| A | 80 | 40 |
| B | 50 | 70 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AC=8,D、E分别为AB、AC的中点,F为线段DE上一点,连接AF、CF使AF⊥CF,且DF=1.若△ADF面积为2,则△ABC的面积为( )
如图,在△ABC中,AC=8,D、E分别为AB、AC的中点,F为线段DE上一点,连接AF、CF使AF⊥CF,且DF=1.若△ADF面积为2,则△ABC的面积为( )| A. | 25 | B. | 30 | C. | 35 | D. | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
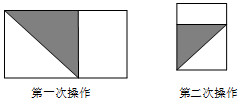 将长为1,宽为a的长方形纸片$({\frac{1}{2}<a<1})$如图那样折一下,剪下一个边长等于长方形的宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如些反复操作下去,若在第n次操作后剩下的长方形为正方形,则操作终止.
将长为1,宽为a的长方形纸片$({\frac{1}{2}<a<1})$如图那样折一下,剪下一个边长等于长方形的宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如些反复操作下去,若在第n次操作后剩下的长方形为正方形,则操作终止.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:(-$\frac{1}{2}$)-1+$\sqrt{3}$tan30°-sin245°
(1)计算:(-$\frac{1}{2}$)-1+$\sqrt{3}$tan30°-sin245°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 节约能源,保护生态,迎接低碳时代的到来,某纸品加工厂利用边角线裁出正方形和长方形两种硬纸片,制作甲、乙两种无盖的长方体纸盒出售给礼品店.
节约能源,保护生态,迎接低碳时代的到来,某纸品加工厂利用边角线裁出正方形和长方形两种硬纸片,制作甲、乙两种无盖的长方体纸盒出售给礼品店.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com