
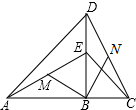
 直角△ABD和直角△EBC如图放置,使点A、B、C在一条直线上,∠ABD=∠EBC=90°,AB=DB,EB=CB,M、N分别是AE、CD的中点.
直角△ABD和直角△EBC如图放置,使点A、B、C在一条直线上,∠ABD=∠EBC=90°,AB=DB,EB=CB,M、N分别是AE、CD的中点.分析 (1)求出△ABE≌△DBC,根据全等三角形的性质得出∠EAB=∠CDB,根据三角形内角和定理求出∠EAB+∠AEB=90°,求出∠DEQ+∠CDB=90°,根据三角形内角和定理求出∠DQE=90°,即可得出答案;
(2)根据全等求出CD=BE,根据直角三角形斜边上中线性质求出即可;
(3)首先证明△CBD≌△EBA可得∠BAE=∠BDC,AE=DC,再根据M,N分别是AE,CD的中点可得DN=AM,然后证明△BMA≌△BND,可得到BM=BN.
解答 (1)证明: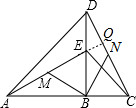
延长AE交CD于Q,
∵在△ABE和△DBC中
$\left\{\begin{array}{l}{AB=BD}\\{∠ABE=∠DBC}\\{BE=BC}\end{array}\right.$
∴△ABE≌△DBC(SAS),
∴∠EAB=∠CDB,
∵∠ABE=90°,
∴∠EAB+∠AEB=90°,∠AEB=∠DEQ,
∴∠DEQ+∠CDB=90°,
∴∠DQE=180°-90°=90°,
∴AE⊥CD;
(2)解:BM=BN,
理由是:∵△ABE≌△DBC,
∴AE=CD,
∵∠ABE=∠DBC=90°,M为AE中点,N为CD中点,
∴BM=$\frac{1}{2}$AE,BN=$\frac{1}{2}$CD,
∴BM=BN;
(3)
解:BM=BN,
理由是:∵∠ABD=∠EBC=90°,
∴∠ABD+∠DBE=∠EBC+∠DBE,
即∠CBD=∠ABE,
在△CBD和△EBA中$\left\{\begin{array}{l}{DB=AB}\\{∠CBD=∠EBA}\\{CB=BE}\end{array}\right.$,
∴△CBD≌△EBA(SAS),
∴∠BAE=∠BDC,AE=DC,
∵M,N分别是AE,CD的中点,
∴DN=AM,
在△BMA和△BND中$\left\{\begin{array}{l}{AM=DN}\\{∠BDN=∠BAM}\\{BD=BA}\end{array}\right.$
∴△BMA≌△BND(SAS),
∴BM=BN.
点评 本题考查了全等三角形的性质和判定,三角形内角和定理,垂直定义,直角三角形斜边上中线性质的应用,关键是掌握判定定理与性质定理.证明三角形全等是证明角相等,线段相等的一种重要的方法,注意:全等三角形的对应边相等,对应角相等,全等三角形的判定定理有SAS,ASA,AAS,SSS.


科目:初中数学 来源: 题型:选择题
| A. | 有两个角相等的三角形 | B. | 有一个角等于45°的直角三角形 | ||
| C. | 三个内角都相等的三角形 | D. | 有一个角等于30°的直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小明和小颖用下面两个转盘做游戏:游戏者同时转动A、B两个转盘,转盘停止后,若一个转盘指针指向红色,另一个转盘指针指向蓝色,则配成了紫色,小明获胜;若指针指向的是同种颜色,则小颖获胜.
如图,小明和小颖用下面两个转盘做游戏:游戏者同时转动A、B两个转盘,转盘停止后,若一个转盘指针指向红色,另一个转盘指针指向蓝色,则配成了紫色,小明获胜;若指针指向的是同种颜色,则小颖获胜.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
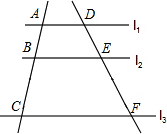 如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F,若AB=1,DE=2,DF=8,则BC的长为( )
如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F,若AB=1,DE=2,DF=8,则BC的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
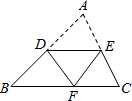 如图,D是AB的中点,将△ABC沿过D的直线折叠,使点A落在BC上的点F处,若∠B=46°,则∠BDF的度数是( )
如图,D是AB的中点,将△ABC沿过D的直线折叠,使点A落在BC上的点F处,若∠B=46°,则∠BDF的度数是( )| A. | 80° | B. | 88° | C. | 92° | D. | 98° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com