
分析 (1)直接利用多项式除以单项式运算法则求出答案;
(2)直接利用平方差公式分解因式进而化简求出答案;
(3)直接利用二次根式以及立方根的定义结合平方差公式化简求出答案;
(4)直接利用平方差公式化简求出答案.
解答 解:(1)(12x3-8x2+16x)÷(-4x)
=-3x2+2x-4;
(2)(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{9{9}^{2}}$)(1-$\frac{1}{10{0}^{2}}$)
=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)(1-$\frac{1}{4}$)(1+$\frac{1}{4}$)…(1-$\frac{1}{100}$)(1+$\frac{1}{100}$)
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×…×$\frac{99}{100}$×$\frac{101}{100}$
=$\frac{1}{2}$×$\frac{101}{100}$
=$\frac{101}{200}$;
(3)$\sqrt{25}$-$\root{3}{8}$-($\sqrt{3}$-2)2($\sqrt{3}$+2)2
=5-2-[($\sqrt{3}$-2)($\sqrt{3}$+2)]2
=3-12
=2;
(4)99×101
=(100-1)×(100+1)
=10000-1
=9999.
点评 此题主要考查了整式的除法运算以及实数运算以及平方差公式的应用,正确应用平方差公式是解题关键.


科目:初中数学 来源: 题型:解答题
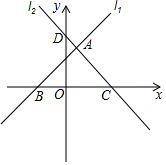 如图所示,在平面直角坐标系中,直线l1:y=x+1与l2:y=-x+2分别交x轴于点B和点C,点D是直线l2与y轴的交点,两直线交于点A.
如图所示,在平面直角坐标系中,直线l1:y=x+1与l2:y=-x+2分别交x轴于点B和点C,点D是直线l2与y轴的交点,两直线交于点A.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
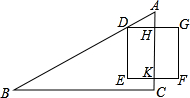 在《九章算术》“勾股”章中有这样一个问题:“今有邑方不知大小,各中开门,出北门二十步有木,出南门十回步,折而西行一千七百七十五步见木,问邑方几何.”用今天的话说,大意是:如图,DEFG是一座正方形小城,北门H位于DG的中点,南门K位于EF的中点,出北门20步到A处有一树木,出南门14步到C,向西行1775步到B处正好看到A处的树木(即点D在直线AB上),小城的边长为多少步,若设小城的边长为2x 步,则可列方程为$\frac{20}{20+14+2x}$=$\frac{x}{1775}$.
在《九章算术》“勾股”章中有这样一个问题:“今有邑方不知大小,各中开门,出北门二十步有木,出南门十回步,折而西行一千七百七十五步见木,问邑方几何.”用今天的话说,大意是:如图,DEFG是一座正方形小城,北门H位于DG的中点,南门K位于EF的中点,出北门20步到A处有一树木,出南门14步到C,向西行1775步到B处正好看到A处的树木(即点D在直线AB上),小城的边长为多少步,若设小城的边长为2x 步,则可列方程为$\frac{20}{20+14+2x}$=$\frac{x}{1775}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
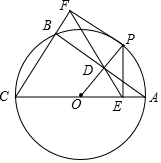 如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线ED交CB的延长线于F点,连接PF.
如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线ED交CB的延长线于F点,连接PF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com