
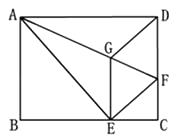
【题目】如图,将矩形ABCD沿线段AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:△AGE≌△AGD
(2)探究线段EG、GF、AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2 ![]() ,求BE的长.
,求BE的长.
【答案】
(1)
证明:∵△AEF是由△ADF折叠得到的,
∴AD=AE,∠DAG=∠EAG,
又∵AG=AG
∴△AGE≌△AGD;
(2)
解:AF×GF=2EG2,
证明如下:
连接DE交GF于点O
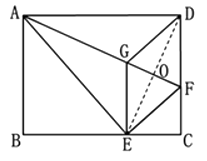
∵△AEF是由△ADF折叠得到的
∠DAG=∠EAG,DF=EF
∵△AGE≌△AGD
∴GD=GE,∠AGD=∠AGE
∴∠FGD=∠FGE
∵EG∥CD
∴∠DFG=∠FGE
∴∠FGD=∠DFG
∴GD=DF
∴GD=EG=EF=DF
∴四边形DGEF是菱形
AF⊥DE,OF= ![]() GF
GF
∴∠ADF=∠DOF=90°
又∵∠DFO=∠DFA
∴△DFO∽△AFD
∴ ![]()
∴OF×AF=DF2
∵OF= ![]() GF,DF=EG
GF,DF=EG
∴ ![]() GF×AF=EG2
GF×AF=EG2
即:AF×GF=2EG2
(3)
解:过点G作GH⊥CD于H

则四边形CHGE是矩形,
∴CE=GH
设GF=x,则AF=6+x
∵AF×GF=2EG2EG=2 ![]()
∴x(6+x)=40
解得:x=4
∴GF=4,
∴AF=6+4=10
在Rt△AEF中
AE= ![]()
∴BC=AD=AE=4 ![]()
∵GH∥AD
∴△FGH∽△FAD
∴ ![]()
∴ ![]()
∴CE=GH= ![]()
∴BE=BC﹣CE=4 ![]() ﹣
﹣ ![]() =
= ![]() .
.
【解析】(1)先依据翻折的性质可得AD=AE,∠DAG=∠EAG,易得△AGE≌△AGD;(2)连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF= ![]() GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系;(3)过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FGH∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD﹣GH求解即可.
GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系;(3)过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FGH∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD﹣GH求解即可.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两名同学在一次用频率去估计概率的实验中,统一了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( ) 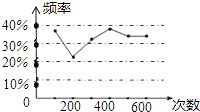
A.从一个装有2个白球和1个红球的袋子中任取两球,取到两个白球的概率
B.任意写一个正整数,它能被2整除的概率
C.抛一枚硬币,连续两次出现正面的概率
D.掷一枚正六面体的骰子,出现1点的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:优秀;B:良好;C:合格;D:一般;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题: 
(1)本次调查中,王老师一共调查了多少名同学?
(2)将上面的条形统计图补充完整;并求出“D”所占的圆心角的度数;
(3)从被调查的A类和D类学生中分别选取一位同学进行“一对一”互助学习,请求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:等腰三角形、平行四边形、菱形、双曲线、抛物线.这些都是我们在初中学习阶段学过的几何图形或函数的图象,那么从它们之中随机抽取两个,得到的都是中心对称图形的概率是( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y= ![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣ ![]() )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( ) 
A.大于0
B.等于0
C.小于0
D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com