
【题目】某加工企业生产并销售某种农产品,假设销售量与加工产量相等.已知每千克生产成本y1(单位:元)与产量x(单位:kg)之间满足表达式y1=![]() 下图中线段AB表示每千克销售价格y2(单位:元)与产量x(单位:kg)之间的函数表达式.
下图中线段AB表示每千克销售价格y2(单位:元)与产量x(单位:kg)之间的函数表达式.
(1)试确定每千克销售价格y2与产量x之间的函数表达式,并写出自变量的取值范围;
(2)若用w(单位:元)表示销售该农产品的利润,试确定w与产量x之间的函数表达式;
(3)求销售量为70 kg时,销售该农产品是赚钱,还是亏本?赚钱或亏本了多少元?

【答案】(1) y2=-x+160(0≤x≤150);(2)①当0≤x<80时,w= -0.5x2+60x,②当80≤x≤150时,w =-4x2+340x; (3)当销售量为70 kg时,销售该农产品是赚钱的,赚了1750元.
【解析】
(1)观察图象可得y2=kx+b的图象过点(0,160)与(150,10),利用待定系数法求得一次函数的解析式即可;(2)分当0≤x<80时和当80≤x≤150时两种情况求w与x之间的函数表达式;(3)把x=70代入(2)中的第一个解析式计算w的值,比较即可解答.
(1)设线段AB所表示的y2与x之间的函数表达式为y2=kx+b,
∵y2=kx+b的图象过点(0,160)与(150,10),
∴![]() 解得
解得![]()
∴y2=-x+160(0≤x≤150).
(2)①当0≤x<80时,w=x[(-x+160)-(-0.5x+100)]=-0.5x2+60x;
②当80≤x≤150时,w=x[(-x+160)-(3x-180)]=-4x2+340x.
w=![]()
(3)∵x=70<80,∴w=-0.5x2+60x=-0.5×702+60×70=1750(元).
∴当销售量为70 kg时,销售该农产品是赚钱的,赚了1750元.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=6.点P在边AC上运动,过点P作PD⊥AB于点D,以AP、AD为邻边作PADE.设□PADE与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x≤6).
(1)求线段PE的长(用含x的代数式表示).
(2)当点E落在边BC上时,求x的值.
(3)求y与x之间的函数关系式.
(4)直接写出点E到△ABC任意两边所在直线距离相等时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣![]() x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣
x+3分别交x轴、y轴于点A、B,P是抛物线y=﹣![]() x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣
x2+2x+5上的一个动点,其横坐标为a,过点P且平行于y轴的直线交直线y=﹣![]() x+3于点Q,则当PQ=BQ时,a的值是_____.
x+3于点Q,则当PQ=BQ时,a的值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.

(1)画出△ABC关于x轴对称的图形△A1B1C1,
(2)写出点A的对应点A1的坐标;
(3)将△ABC的横、纵坐标分别乘以-1,画出对应的图形△A2B2C2;若P(a,b)为△ABC边上一点,则在△A2B2C2中,点P对应的点Q的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 与一次函数y=x+b的图象交于A(1,-k+4),B(k-4,-1)两点.
与一次函数y=x+b的图象交于A(1,-k+4),B(k-4,-1)两点.
(1)试确定这两个函数的表达式;
(2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一多边形草坪,在市政建设设计图纸上的面积为300cm2,其中一条边的长度为5cm.经测量,这条边的实际长度为15m,则这块草坪的实际面积是( )
A. 100m2 B. 270m2 C. 2700m2 D. 90000m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形。用A种纸片张,B种纸片一张,C种纸片两张可拼成如图2的大正方形.

(1)请用两种不同的方法求图2大正方形的面积(答案直接填写到题中横线上);
方法1____________;方法2_____________;
(2)观察图2,请你直接写出下列三个代数式: (a+b)![]() , a
, a![]() +b
+b![]() ,ab之间的等量关系_____________;
,ab之间的等量关系_____________;
(3)类似的,请你用图1中的三种纸片拼一个图形验证:(a+b)(a+2b)=a![]() +3ab+2b
+3ab+2b![]() ;
;
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=6, a![]() +b
+b![]() =14,求ab的值;
=14,求ab的值;
②已知(x2018)![]() +(x2020)
+(x2020)![]() =34,求(x2019)
=34,求(x2019)![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=x+m的图象交y轴于点D,且它与正比例函数![]() 的图象交于点A(2,n),设x轴上有一点P,过点P作x轴的垂线(垂线位于点A的右侧),分别交
的图象交于点A(2,n),设x轴上有一点P,过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和y=x+m的图象与点B、C.
和y=x+m的图象与点B、C.
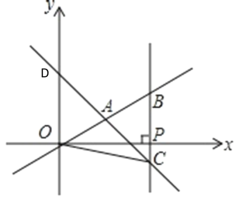
(1)求m和n的值;
(2)若BC=OD,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.
(1)求证:DF∥AO;
(2)若AC=6,AB=10,求CG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com