
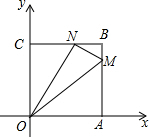
 如图,在平面直角坐标系中,四边形OABC是边长为4的正方形,M(4,m)、N(n,4)分别是AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=5.
如图,在平面直角坐标系中,四边形OABC是边长为4的正方形,M(4,m)、N(n,4)分别是AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=5. 分析 证明△OCN∽△NBM,列比例式得:m=$\frac{1}{4}{n}^{2}-n+4$=$\frac{1}{4}$(n-2)2+3,即当n=2时,m有最小值为3,在Rt△OAM中,因为OA是定值,AM的大小决定OM的大小,由m的最小值计算OM的最小值.
解答 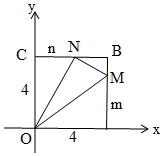 解:由题意得:OA=4,AM=m,OC=4,CN=n,BN=4-n,BM=4-m,
解:由题意得:OA=4,AM=m,OC=4,CN=n,BN=4-n,BM=4-m,
∵四边形OABC是矩形,
∴∠OCB=∠ABC=90°,
∴∠CNO+∠CON=90°,
∵ON⊥MN,
∴∠ONM=90°,
∴∠CNO+∠MNB=90°,
∴∠CON=∠MNB,
∴△OCN∽△NBM,
∴$\frac{OC}{NB}=\frac{CN}{BM}$,
∴$\frac{4}{4-n}$=$\frac{n}{4-m}$,
m=$\frac{1}{4}{n}^{2}-n+4$=$\frac{1}{4}$(n-2)2+3,
即当n=2时,m有最小值为3,
在Rt△OAM中,OA是定值,AM的大小决定OM的大小,
当AM为最小时,OM为最小,
∴当AM=m=3时,OM最小,此时m+n=3+2=5,
故答案为:5.
点评 本题考查了正方形的性质、坐标与图形的性质、相似三角形的性质和判定以及二次函数的最值问题,本题与二次函数相结合,利用二次函数的最值来解决直角三角形的斜边的最值问题.


科目:初中数学 来源: 题型:选择题
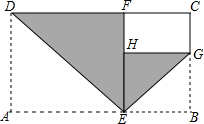 如图,长方形纸片ABCD,AB=a,BC=b,且b<a<2b,则∠ADC的平分线DE折叠纸片,点A落在CD边上的点F处,再沿∠BEF的平分线EG折叠纸片,点B落在EF边上的点H处,则四边形CGHF的周长是( )
如图,长方形纸片ABCD,AB=a,BC=b,且b<a<2b,则∠ADC的平分线DE折叠纸片,点A落在CD边上的点F处,再沿∠BEF的平分线EG折叠纸片,点B落在EF边上的点H处,则四边形CGHF的周长是( )| A. | 2a | B. | 2b | C. | 2(a-b) | D. | a+b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 太极图的形状为阴阳两鱼互纠在一起(如图),象征两极和合.太极图中的白色部分作怎样的变换,可得到黑色部分?若整个圆的直径为6cm,求出图中黑色部分的面积?
太极图的形状为阴阳两鱼互纠在一起(如图),象征两极和合.太极图中的白色部分作怎样的变换,可得到黑色部分?若整个圆的直径为6cm,求出图中黑色部分的面积?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$$+\sqrt{2}$=2 | B. | 3+$\sqrt{2}$=3$\sqrt{2}$ | C. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | D. | $\sqrt{9}$+$\sqrt{3}$=3$+\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com