
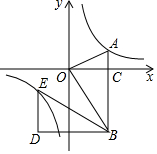
 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.
如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.分析 (1)将点A($\sqrt{3}$,1)代入y=$\frac{k}{x}$,利用待定系数法即可求出反比例函数的表达式;根据射影定理求出BC=3,那么B($\sqrt{3}$,-3);
(2)先解△OAB,得出∠ABO=30°,再根据旋转的性质求出E点坐标为(-$\sqrt{3}$,-1),即可求解.
解答 解:(1)∵点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.
∴k=$\sqrt{3}$×1=$\sqrt{3}$,
∴反比例函数的表达式为y=$\frac{\sqrt{3}}{x}$;
∵A($\sqrt{3}$,1),AB⊥x轴于点C,
∴OC=$\sqrt{3}$,AC=1,
∵OA⊥OB,
由射影定理得OC2=AC•BC,可得BC=3,B($\sqrt{3}$,-3),
(2)点E在该反比例函数的图象上,理由如下:
∵OA⊥OB,OA=2,OB=2$\sqrt{3}$,AB=4,
∴sin∠ABO=$\frac{OA}{AB}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴∠ABO=30°,
∵将△BOA绕点B按逆时针方向旋转60°得到△BDE,
∴△BOA≌△BDE,∠OBD=60°,
∴BO=BD=2$\sqrt{3}$,OA=DE=2,∠BOA=∠BDE=90°,∠ABD=30°+60°=90°,
而BD-OC=$\sqrt{3}$,BC-DE=1,
∴E(-$\sqrt{3}$,-1),
∵-$\sqrt{3}$×(-1)=$\sqrt{3}$,
∴点E在该反比例函数的图象上.
点评 本题考查了待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征,旋转的性质,正确求出解析式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
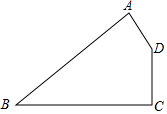 如图,四边形ABCD是某新建厂区示意图,∠A=75°,∠B=45°,BC⊥CD,AB=500$\sqrt{2}$米,AD=200米,现在要在厂区四周建围墙,求围墙的长度有多少米?
如图,四边形ABCD是某新建厂区示意图,∠A=75°,∠B=45°,BC⊥CD,AB=500$\sqrt{2}$米,AD=200米,现在要在厂区四周建围墙,求围墙的长度有多少米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
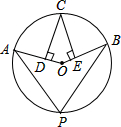 如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=36°,则∠P的度数为( )
如图,点A,B,C,P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=36°,则∠P的度数为( )| A. | 144° | B. | 72° | C. | 60° | D. | 36° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
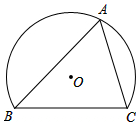 如图,弓形ABC中,∠BAC=60°,BC=2$\sqrt{3}$.若点P在优弧BAC上由点B移动到点C,记△PBC的内心为I,点I随点P的移动所经过的路径长为( )
如图,弓形ABC中,∠BAC=60°,BC=2$\sqrt{3}$.若点P在优弧BAC上由点B移动到点C,记△PBC的内心为I,点I随点P的移动所经过的路径长为( )| A. | $\frac{2}{3}$π | B. | $\frac{4}{3}$π | C. | $\frac{8}{3}$π | D. | 4π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com