
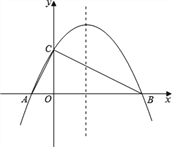
【题目】如图,已知抛物线![]() 与x轴相交于A、B两点,与y轴相交于点C(0,4),若已知A点的坐标为A(﹣2,0).
与x轴相交于A、B两点,与y轴相交于点C(0,4),若已知A点的坐标为A(﹣2,0).
(1)求抛物线的解析式;
(2)求△ABC的外接圆圆心坐标;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标,若不存在,请说明理由.
【答案】(1)![]() ;(2) 圆心坐标为(3,0);(3)见解析.
;(2) 圆心坐标为(3,0);(3)见解析.
【解析】分析:
(1)将A、C两点的坐标代入抛物线的解析式列出关于b、c的方程组,解方程组求得b、c的值即可得到所求解析式;
(2)由(1)中所得解析式先求出点B的坐标,再结合点A、C的坐标求得线段AC、BC、AB的长,由勾股定理的逆定理证得∠ACB=90°,由此即可得到△ABC的外心是斜边AB的中点,由此即可得到所求坐标;
(3)由(1)中所得抛物线的解析式可求得抛物线的对称轴为直线x=3,设点Q的坐标为(3,t),结合点A、C的坐标可将AC、AQ和CQ的长度表达出来,然后分AQ=CQ、AC=CQ和AQ=AC三种情况列出方程,解方程即可求得符合条件的点Q的坐标.
详解:
(1)∵抛物线![]() 的图象经过点A(﹣2,0),C(0,4)
的图象经过点A(﹣2,0),C(0,4)
∴ 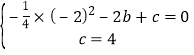
解得:b=![]() ,c=4
,c=4
∴抛物线解析式为![]() ;
;
(2)在![]() 中,令y=0,即
中,令y=0,即![]() ,
,
整理得x2﹣6x﹣16=0,解得:x=8或x=﹣2,
∴A(﹣2,0),B(8,0),
∴OA=2,OC=4,OB=8,AB=10,
∴![]()
![]()
![]() ,
,
∴![]()
∴△ABC是直角三角形,且![]() ,
,
∴△ABC的外接圆圆心在AB边上的中点处,圆心坐标为(3,0),

(3)∵![]() ,
,
∴抛物线的线的对称轴为:x=3,
可设点Q(3,t),∵点A、C的坐标分别为(-2,0)和(0,4),
∴AC=![]() ,AQ=
,AQ=![]() ,CQ=
,CQ=![]() ,
,
i)当AQ=CQ时,
有![]() ,即25+t2=t2﹣8t+16+9,
,即25+t2=t2﹣8t+16+9,
解得t=0,
∴Q1(3,0);
ii)当AC=AQ时,
有![]() ,即
,即![]() ,此方程无实数根,
,此方程无实数根,
∴此时△ACQ不能构成等腰三角形;
iii)当AC=CQ时,
有![]() ,即:t2﹣8t+5=0,
,即:t2﹣8t+5=0,
解得:t=4±![]() ,
,
∴点Q坐标为:Q2(3,4+![]() ),Q3(3,4﹣
),Q3(3,4﹣![]() ).
).
综上所述,存在点Q,使△ACQ为等腰三角形,点Q的坐标为:Q1(3,0),Q2(3,4+![]() ),Q3(3,4﹣
),Q3(3,4﹣![]() ).
).


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】
如图,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( )
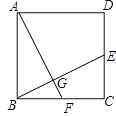
A.BE=AF B.∠DAF=∠BEC C.∠AFB+∠BEC=90° D.AG⊥BE
查看答案和解析>>
科目:初中数学 来源: 题型:
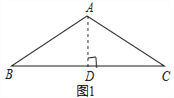
【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°,于是
∠BAC=60°,于是![]() ;
;
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
(1)求证:△ADB≌△AEC;
(2)若AD=2,BD=3,请计算线段CD的长;
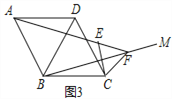
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
(3)证明:△CEF是等边三角形;
(4)若AE=4,CE=1,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简:
(1)10﹣(﹣5)+(﹣9)+6;
(2)﹣14﹣5×[2﹣(﹣3)2];
(3)﹣2+(﹣![]() )×(﹣
)×(﹣![]() )+(﹣
)+(﹣![]() )×
)×![]()
(4)|π-4|+|3-π|.
查看答案和解析>>
科目:初中数学 来源: 题型:
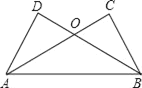
【题目】如图,AC⊥BC,AD⊥DB,下列条件中: ①∠ABD=∠BAC;②∠DAB=∠CBA;③AD=BC;④∠DAC=∠CBD,能使△ABC≌△BAD的有_____(把所有正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
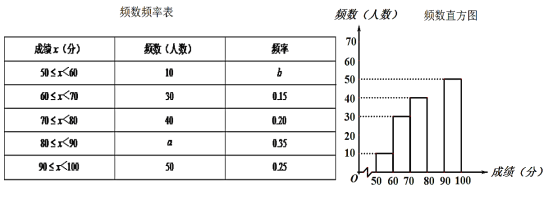
【题目】为传承中华优秀传统文化,某校团委组织了一次全校![]() 名学生参加的“汉字书写”大赛,为了解本次大赛的成绩,校团委随机抽取了其中
名学生参加的“汉字书写”大赛,为了解本次大赛的成绩,校团委随机抽取了其中![]() 名学生的成绩(成绩
名学生的成绩(成绩![]() 取整数,总分
取整数,总分![]() 分)作为样本进行统计,制成如下不完整的统计图表:
分)作为样本进行统计,制成如下不完整的统计图表:
根据所给信息,解答下列问题:
(1)![]() _____,
_____,![]() ______;
______;
(2)补全频数直方图;
(3)这![]() 名学生成绩的中位数会落在______分数段;
名学生成绩的中位数会落在______分数段;
(4)若成绩在![]() 分以上(包括
分以上(包括![]() 分)为“优”等,请你估计该校参加本次比赛的
分)为“优”等,请你估计该校参加本次比赛的![]() 名学生中成绩为“优”等的有多少人。
名学生中成绩为“优”等的有多少人。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
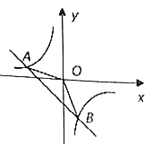
(1)试确定上述反比例函数和一次函数的表达式;
(2)当![]() 为何值时反比例函数值大于一次函数的值;
为何值时反比例函数值大于一次函数的值;
(3)当![]() 为何值时一次函数值大于比例函数的值;
为何值时一次函数值大于比例函数的值;
(4)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() 给出定义如下:我们称使等式a﹣b=2ab﹣1成立的一对有理数a,b为“同心有理数对”,记为(a,b),如:数对(1,
给出定义如下:我们称使等式a﹣b=2ab﹣1成立的一对有理数a,b为“同心有理数对”,记为(a,b),如:数对(1,![]() ),(2,
),(2,![]() ),都是“同心有理数对”.
),都是“同心有理数对”.
(1)数对(﹣2,1),(3,![]() )是 “同心有理数对”的是__________.
)是 “同心有理数对”的是__________.
(2)若(a,3)是“同心有理数对”,求a的值;
(3)若(m,n)是“同心有理数对”,则(﹣n,﹣m) “同心有理数对”(填“是”或“不是”),说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com