
”¾ĢāÄæ”æÉčĖ«ĒśĻßy£½![]() £Øk£¾0£©ÓėÖ±Ļßy£½x½»ÓŚA\BĮ½µć£ØµćAŌŚµŚČżĻóĻŽ£©£¬½«Ė«ĒśĻßŌŚµŚŅ»ĻóĻŽµÄŅ»Ö§ŃŲÉäĻßBAµÄ·½ĻņĘ½ŅĘ£¬Ź¹Ęä¾¹żµćA£¬½«Ė«ĒśĻßŌŚµŚČżĻóĻŽµÄŅ»Ö§ŃŲÉäĻßABµÄ·½ĻņĘ½ŅĘ£¬Ź¹Ęä¾¹żµćB£¬Ę½ŅĘŗóµÄĮ½ĢõĒśĻßĻą½»ÓŚP”¢QĮ½µć£¬“ĖŹ±ĪŅĆĒ³ĘĘ½ŅĘŗóµÄĮ½ĢõĒśĻßĖłĪ§²æ·Ö£ØČēĶ¼ÖŠŅõÓ°²æ·Ö£©ĪŖĖ«ĒśĻߵĔ°ķų”±£¬PQĪŖĖ«ĒśĻߵĔ°ķų¾¶”°£¬µ±Ė«ĒśĻßy£½
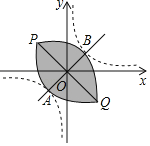
£Øk£¾0£©ÓėÖ±Ļßy£½x½»ÓŚA\BĮ½µć£ØµćAŌŚµŚČżĻóĻŽ£©£¬½«Ė«ĒśĻßŌŚµŚŅ»ĻóĻŽµÄŅ»Ö§ŃŲÉäĻßBAµÄ·½ĻņĘ½ŅĘ£¬Ź¹Ęä¾¹żµćA£¬½«Ė«ĒśĻßŌŚµŚČżĻóĻŽµÄŅ»Ö§ŃŲÉäĻßABµÄ·½ĻņĘ½ŅĘ£¬Ź¹Ęä¾¹żµćB£¬Ę½ŅĘŗóµÄĮ½ĢõĒśĻßĻą½»ÓŚP”¢QĮ½µć£¬“ĖŹ±ĪŅĆĒ³ĘĘ½ŅĘŗóµÄĮ½ĢõĒśĻßĖłĪ§²æ·Ö£ØČēĶ¼ÖŠŅõÓ°²æ·Ö£©ĪŖĖ«ĒśĻߵĔ°ķų”±£¬PQĪŖĖ«ĒśĻߵĔ°ķų¾¶”°£¬µ±Ė«ĒśĻßy£½![]() £Øk£¾0£©µÄķų¾¶ĪŖ6Ź±£¬kµÄÖµĪŖ£Ø””””£©
£Øk£¾0£©µÄķų¾¶ĪŖ6Ź±£¬kµÄÖµĪŖ£Ø””””£©
A.![]() B.2C.
B.2C.![]() D.3
D.3
”¾“š°ø”æA
”¾½āĪö”æ
ŅŌPQĪŖ±ß£¬×÷¾ŲŠĪPQQ”äP”ä½»Ė«ĒśĻßÓŚµćP”䔢Q”䣬ĮŖĮ¢Ö±ĻßAB¼°Ė«ĒśĻß½āĪöŹ½³É·½³Ģ×飬Ķعż½ā·½³Ģ×éæÉĒó³öµćA”¢BµÄ×ų±ź£¬ÓÉPQµÄ³¤¶ČæÉµĆ³öµćPµÄ×ų±ź£ØµćPŌŚÖ±Ļßy£½xÉĻ£©£¬ÓÉĶ¼ŠĪµÄ¶Ō³ĘŠŌ½įŗĻµćA”¢BŗĶPµÄ×ų±źæÉµĆ³öµćP”äµÄ×ų±ź£¬ŌŁĄūÓĆ·“±ČĄżŗÆŹżĶ¼ĻóÉĻµćµÄ×ų±źĢŲÕ÷¼“æÉµĆ³ö¹ŲÓŚkµÄŅ»ŌŖŅ»“Ī·½³Ģ£¬½āÖ®¼“æÉµĆ³ö½įĀŪ£®
ŅŌPQĪŖ±ß£¬×÷¾ŲŠĪPQQ”äP”ä½»Ė«ĒśĻßÓŚµćP”䔢Q”䣬ČēĶ¼ĖłŹ¾£®
ĮŖĮ¢Ö±ĻßAB¼°Ė«ĒśĻß½āĪöŹ½³É·½³Ģ×飬![]() £¬
£¬
½āµĆ£ŗ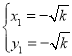 £¬
£¬ £¬
£¬
”ąµćAµÄ×ų±źĪŖ£Ø©![]() £¬©
£¬©![]() £©£¬µćBµÄ×ų±źĪŖ£Ø
£©£¬µćBµÄ×ų±źĪŖ£Ø![]() £¬
£¬![]() £©£®
£©£®
”ßPQ£½6£¬
”ąOP£½3£¬µćPµÄ×ų±źĪŖ£Ø©![]() £¬
£¬![]() £©£®
£©£®
øł¾ŻĶ¼ŠĪµÄ¶Ō³ĘŠŌæÉÖŖ£ŗPP”䣽AB£½QQ”䣬
”ąµćP”äµÄ×ų±źĪŖ£Ø©![]() +2
+2![]() £¬
£¬![]() +2
+2![]() £©£®
£©£®
Ó֔ߵćP”äŌŚĖ«ĒśĻßy£½![]() ÉĻ£¬
ÉĻ£¬
”ą£Ø©![]() +2
+2![]() £©£Ø
£©£Ø![]() +2
+2![]() £©£½k£¬
£©£½k£¬
½āµĆ£ŗk£½![]() £®
£®
¹ŹŃ”£ŗA£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
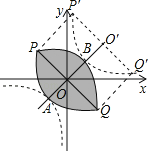
”¾ĢāÄæ”æČēĶ¼£¬Ö±ĻßABÓė![]() Öį½»ÓŚµćA£¬Óė
Öį½»ÓŚµćA£¬Óė![]() Öį½»ÓŚµćB£¬ÓėĖ«ĒśĻß
Öį½»ÓŚµćB£¬ÓėĖ«ĒśĻß![]() (
(![]() )½»ÓŚµćC£¬¹żµćC×÷CD”Ķ
)½»ÓŚµćC£¬¹żµćC×÷CD”Ķ![]() ÖįÓŚµćD£¬¹żµćB×÷BE”ĶCDÓŚµćE£¬tan”ĻBCE=
ÖįÓŚµćD£¬¹żµćB×÷BE”ĶCDÓŚµćE£¬tan”ĻBCE=![]() ,µćEµÄ×ų±źĪŖ(2£¬
,µćEµÄ×ų±źĪŖ(2£¬![]() )£¬Į¬½ÓAE£®
)£¬Į¬½ÓAE£®
£Ø1£©Ēó![]() µÄÖµ£»
掙术
£Ø2£©Ēó”÷ACEµÄĆ껿 £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
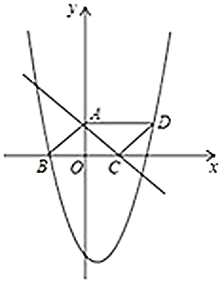
”¾ĢāÄæ”æČēĶ¼£¬Čż½ĒŠĪ![]() ŹĒŅŌ
ŹĒŅŌ![]() ĪŖµ×±ßµÄµČŃüČż½ĒŠĪ£¬µć
ĪŖµ×±ßµÄµČŃüČż½ĒŠĪ£¬µć![]() ”¢
”¢![]() ·Ö±šŹĒŅ»“ĪŗÆŹż
·Ö±šŹĒŅ»“ĪŗÆŹż![]() µÄĶ¼ĻóÓė
µÄĶ¼ĻóÓė![]() Öį”¢
Öį”¢![]() ÖįµÄ½»µć£¬µć
ÖįµÄ½»µć£¬µć![]() ŌŚ¶ž“ĪŗÆŹż
ŌŚ¶ž“ĪŗÆŹż![]() µÄĶ¼ĻóÉĻ£¬ĒŅøƶž“ĪŗÆŹżĶ¼ĻóÉĻ“ęŌŚŅ»µć
µÄĶ¼ĻóÉĻ£¬ĒŅøƶž“ĪŗÆŹżĶ¼ĻóÉĻ“ęŌŚŅ»µć![]() Ź¹ĖıߊĪ
Ź¹ĖıߊĪ![]() Äܹ¹³ÉĘ½ŠŠĖıߊĪ.
Äܹ¹³ÉĘ½ŠŠĖıߊĪ.
£Ø1£©ŹŌĒó![]() ”¢
”¢![]() µÄÖµ£¬²¢Š“³öøƶž“ĪŗÆŹż±ķ“ļŹ½£»
µÄÖµ£¬²¢Š“³öøƶž“ĪŗÆŹż±ķ“ļŹ½£»
£Ø2£©¶Æµć![]() ŃŲĻ߶Ī
ŃŲĻ߶Ī![]() “Ó
“Ó![]() µ½
µ½![]() £¬Ķ¬Ź±¶Æµć
£¬Ķ¬Ź±¶Æµć![]() ŃŲĻ߶Ī
ŃŲĻ߶Ī![]() “Ó
“Ó![]() µ½
µ½![]() ¶¼ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŌĖ¶Æ£¬ĪŹ£ŗ
¶¼ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŌĖ¶Æ£¬ĪŹ£ŗ
¢Łµ±![]() ŌĖ¶Æ¹ż³ĢÖŠÄÜ·ń“ęŌŚ
ŌĖ¶Æ¹ż³ĢÖŠÄÜ·ń“ęŌŚ![]() £æČē¹ū²»“ęŌŚĒėĖµĆ÷ĄķÓÉ£»Čē¹ū“ęŌŚĒėĖµĆ÷µćµÄĪ»ÖĆ£æ
£æČē¹ū²»“ęŌŚĒėĖµĆ÷ĄķÓÉ£»Čē¹ū“ęŌŚĒėĖµĆ÷µćµÄĪ»ÖĆ£æ
¢Śµ±![]() ŌĖ¶Æµ½ŗĪ“¦Ź±£¬ĖıߊĪ
ŌĖ¶Æµ½ŗĪ“¦Ź±£¬ĖıߊĪ![]() µÄĆ껿×īŠ”£æ“ĖŹ±ĖıߊĪ
µÄĆ껿×īŠ”£æ“ĖŹ±ĖıߊĪ![]() µÄĆ껿ŹĒ¶ąÉŁ£æ
µÄĆ껿ŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚµČ±ß”÷ABCÖŠ£¬PĪŖBCÉĻŅ»µć£¬DĪŖACÉĻŅ»µć£¬ĒŅ”ĻAPD£½60”ć£¬BP£½2£¬CD£½1£¬Ōņ”÷ABCµÄ±ß³¤ĪŖ£Ø””””£©
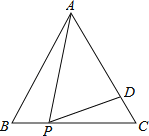
A.3B.4C.5D.6
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗ”÷ABCŌŚÖ±½Ē×ų±źĘ½ĆęÄŚ£¬Čżøö¶„µćµÄ×ų±ź·Ö±šĪŖA£Ø0£¬3£©”¢B£Ø3£¬4£©”¢C£Ø2£¬2£©£ØÕż·½ŠĪĶųøńÖŠĆæøöŠ”Õż·½ŠĪµÄ±ß³¤ŹĒŅ»øöµ„Ī»³¤¶Č£©£®
£Ø1£©»³ö”÷ABCĻņĻĀĘ½ŅĘ4øöµ„Ī»³¤¶ČµĆµ½µÄ”÷A1B1C1£¬µćC1µÄ×ų±źŹĒ”” ””£»
£Ø2£©ŅŌµćBĪŖĪ»ĖĘÖŠŠÄ£¬ŌŚĶųøńÄŚ»³ö”÷A2B2C2£¬Ź¹”÷A2B2C2Óė”÷ABCĪ»ĖĘ£¬ĒŅĪ»ĖʱČĪŖ2£ŗ1£»
£Ø3£©ĖıߊĪAA2C2CµÄĆ껿ŹĒ”” ””Ę½·½µ„Ī»£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø1£©±ß³¤·Ö±šĪŖ5£¬12£¬13µÄČż½ĒŠĪÄŚĒŠŌ²°ė¾¶ŹĒ £»
£Ø2£©ČōĖıߊĪABCD“ęŌŚÄŚĒŠŌ²£ØÓėø÷±ß¶¼ĻąĒŠµÄŌ²£©£¬ČēĶ¼2ĒŅĆ껿ĪŖS£¬ø÷±ß³¤·Ö±šĪŖa£¬b£¬c£¬d£¬ŹŌĶʵ¼ĖıߊĪµÄÄŚĒŠŌ²°ė¾¶¹«Ź½£»
£Ø3£©ČōŅ»øön±ßŠĪ£ØnĪŖ²»Š”ÓŚ3µÄÕūŹż£©“ęŌŚÄŚĒŠŌ²£¬ĒŅĆ껿ĪŖS£¬ø÷±ß³¤·Ö±šĪŖa1£¬a2£¬a3£¬”£¬an£¬ŗĻĄķ²ĀĻėĘäÄŚĒŠŌ²°ė¾¶¹«Ź½£Ø²»ŠčĖµĆ÷ĄķÓÉ£©£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻBAC=90”ć£¬AB=AC=10cm£¬µćDĪŖ”÷ABCÄŚŅ»µć£¬”ĻBAD=15”ć£¬AD=6cm£¬Į¬½ÓBD£¬½«”÷ABDČʵćAÄꏱÕė·½ĻņŠż×Ŗ£¬Ź¹ABÓėACÖŲŗĻ£¬µćDµÄ¶ŌÓ¦µćE£¬Į¬½ÓDE£¬DE½»ACÓŚµćF£¬ŌņCFµÄ³¤ĪŖ________cm.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
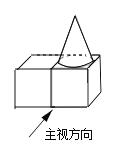
”¾ĢāÄæ”浄ææ”°ĖĄ”±¼Ē»¹²»ŠŠ,»¹µĆ”°»ī”±ÓĆ,¹ĆĒŅ³ĘÖ®ĪŖ”°ĻČĖĄŗó»ī”±°É”£ČĆѧɜ°ŃŅ»ÖÜ擵½»ņĢżµ½µÄŠĀĻŹŹĀ¼ĒĻĀĄ“,ŽšĘśÄĒŠ©¼Ł»°Ģ×»°æÕ»°,Š“³ö×Ō¼ŗµÄÕęĒ鏵øŠ,ĘŖ·łæɳ¤æɶĢ,²¢ŅŖĒóŌĖÓĆ»żĄŪµÄ³ÉÓļ”¢ĆūŃŌ¾Æ¾äµČ,¶ØĘŚ¼ģ²éµćĘĄ,Ń”ŌńÓÅŠćĘŖÄæŌŚ°ąĄļĄŹ¶Į»ņÕ¹³ö”£ÕāŃł,¼“¹®¹ĢĮĖĖłŃ§µÄ²ÄĮĻ,ÓÖ¶ĶĮ¶ĮĖѧɜµÄŠ“×÷ÄÜĮ¦,Ķ¬Ź±»¹ÅąŃųĮĖѧɜµÄ¹Ū²ģÄÜĮ¦”¢Ė¼Ī¬ÄÜĮ¦µČµČ,“ļµ½”°Ņ»ŹÆ¶ąÄń”±µÄŠ§¹ū”£ ČēĶ¼£¬ÓÉĮ½øöĻąĶ¬µÄÕż·½ĢåŗĶŅ»øöŌ²×¶Ģå×é³ÉŅ»øöĮ¢ĢåĶ¼ŠĪ£¬Ęä×óŹÓĶ¼ŹĒ£Ø £©
A.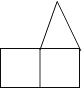 B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µČŃüÖ±½Ē”÷ABCÖŠ£¬CA=CB£¬µćEĪŖ”÷ABCĶāŅ»µć£¬CE=CA£¬ĒŅCDĘ½·Ö”ĻACB½»AEÓŚD£¬ĒŅ”ĻCDE=60”ć£®
£Ø1£©ĒóÖ¤£ŗ”÷CBEĪŖµČ±ßČż½ĒŠĪ£»
£Ø2£©ČōAD=5£¬DE=7£¬ĒóCDµÄ³¤£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com