
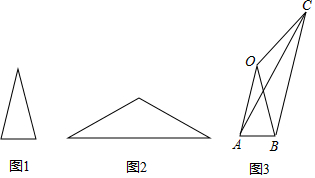
| A. | ∠OCB=2∠ACB | B. | ∠OAB+∠OAC=90° | C. | AC=2$\sqrt{15}$ | D. | BC=4$\sqrt{3}$ |
分析 A、根据∠OBC=∠AOB即可得出OA∥BC,由平行线的性质即可得出∠OAC=∠ACB,再由等腰三角形的性质即可得出∠OAC=∠OCA,替换后即可得出∠OCB=2∠ACB,结论A正确;B、根据等腰三角形的性质结合三角形内角和定理即可得出∠OAB+$\frac{1}{2}$∠AOB=90°,结合结论A即可得出∠OAB+∠OAC=90°,结论B正确;C、过点O作OE⊥AB于点E,过点O作OF⊥AC于点F,则△AOE≌△OAE,利用勾股定理即可AF=OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=$\sqrt{15}$,从而得出AC=2AF=2$\sqrt{15}$,结论C正确;D、过点B作BM⊥OA于点M,过点O作ON⊥BC于点N,则△AOE∽△ABM,根据相似三角形的性质即可得出AM=$\frac{1}{2}$,OM=AO-AM=$\frac{7}{2}$,由BC∥AO、BM⊥AO、ON⊥BC即可得出四边形MBNO为矩形,再根据矩形的性质以及等腰三角形的性质即可得出BC=2BN=2OM=7,结论D错误.综上即可得出结论.
解答 解:A、∵∠OBC=∠AOB,
∴OA∥BC,
∴∠OAC=∠ACB.
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OCA=∠ACB,
∴∠OCB=2∠ACB,结论A正确;
B、∵OA=OB,
∴∠OAB+∠AOB+∠OBA=180°.
∵∠OAC=$\frac{1}{2}$∠OCB=$\frac{1}{2}$∠AOB,∠OAB=∠OBA,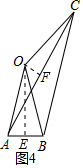
∴∠OAB+$\frac{1}{2}$∠AOB=90°,即∠OAB+∠OAC=90°,结论B正确;
C、过点O作OE⊥AB于点E,过点O作OF⊥AC于点F,如图4所示.
∵OA=OB,
∴∠AOE=$\frac{1}{2}$∠AOB=∠OAE.
在△AOE和△OAE中,$\left\{\begin{array}{l}{∠AOE=∠OAF}\\{∠AEO=∠OFA}\\{AO=OA}\end{array}\right.$,
∴△AOE≌△OAE(AAS),
∴AF=OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=$\sqrt{15}$,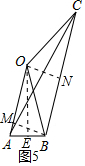
∴AC=2AF=2$\sqrt{15}$,结论C正确;
D、过点B作BM⊥OA于点M,过点O作ON⊥BC于点N,如图5所示.
∵∠OAB+∠AOE=90°,∠MAB+∠ABM=90°,
∴∠AOE=∠ABM.
∵∠AEO=∠AMB=90°,
∴△AOE∽△ABM,
∴$\frac{AM}{AE}=\frac{AB}{AO}$,
∴AM=$\frac{1}{2}$,OM=AO-AM=$\frac{7}{2}$.
∵BC∥AO,BM⊥AO,ON⊥BC,
∴四边形MBNO为矩形,
∴BN=OM=$\frac{7}{2}$.
∵OB=OC,ON⊥BC,
∴BC=2BN=7,结论D错误.
故选D.
点评 本题考查了等腰三角形的性质、解直角三角形、相似三角形的判定与性质、全等三角形的判定与性质以及矩形的判定与性质,逐一分析四个选项的正误是解题的关键.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
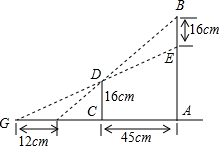 如图,明珠大厦的顶部建有一直径为16m的“明珠”,它的西面45m处有一高16m的小型建筑CD,人站在CD的西面附近无法看到“明珠”的外貌,如果向西走到点F处,可以开始看到“明珠”的顶端B;若想看到“明珠”的全貌,必须往西至少再走12m,求大厦主体建筑的高度AE(不含顶部的“明珠”部分的高度)
如图,明珠大厦的顶部建有一直径为16m的“明珠”,它的西面45m处有一高16m的小型建筑CD,人站在CD的西面附近无法看到“明珠”的外貌,如果向西走到点F处,可以开始看到“明珠”的顶端B;若想看到“明珠”的全貌,必须往西至少再走12m,求大厦主体建筑的高度AE(不含顶部的“明珠”部分的高度)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
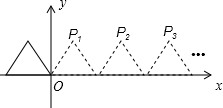 如图,将边长为2的等边三角形沿x轴正方形连续翻折2014次,依次得到点P1、P2、P3、…、P2014,则点P2014的坐标是(4027,$\sqrt{3}$).
如图,将边长为2的等边三角形沿x轴正方形连续翻折2014次,依次得到点P1、P2、P3、…、P2014,则点P2014的坐标是(4027,$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “十一黄金周”期间,小明一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
“十一黄金周”期间,小明一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com