
【题目】如图1,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
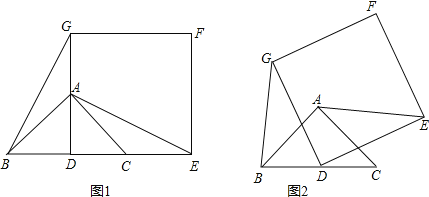
(1)试猜想线段BG和AE的数量关系是 ;
(2)将正方形DEFG绕点D逆时针方向旋转α(0°<α≤360°),
①判断(1)中的结论是否仍然成立?请利用图2证明你的结论;
②若BC=DE=4,当AE取最大值时,求AF的值.
【答案】(1)BG=AE;(2)①见解析;②AF=2![]() .
.
【解析】
试题分析:(1)由等腰直角三角形的性质及正方形的性质就可以得出△ADE≌△BDG就可以得出结论;
(2)①如图2,连接AD,由等腰直角三角形的性质及正方形的性质就可以得出△ADE≌△BDG就可以得出结论;
②由①可知BG=AE,当BG取得最大值时,AE取得最大值,由勾股定理就可以得出结论.
解:(1)BG=AE.
理由:如图1,∵△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,
∴AD⊥BC,BD=CD,
∴∠ADB=∠ADC=90°.
∵四边形DEFG是正方形,
∴DE=DG.
在△BDG和△ADE中,
 ,
,
∴△ADE≌△BDG(SAS),
∴BG=AE.
故答案为:BG=AE;
(2)①成立BG=AE.
理由:如图2,连接AD,
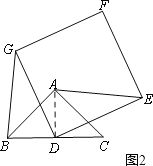
∵在Rt△BAC中,D为斜边BC中点,
∴AD=BD,AD⊥BC,
∴∠ADG+∠GDB=90°.
∵四边形EFGD为正方形,
∴DE=DG,且∠GDE=90°,
∴∠ADG+∠ADE=90°,
∴∠BDG=∠ADE.
在△BDG和△ADE中,
 ,
,
∴△BDG≌△ADE(SAS),
∴BG=AE;
②∵BG=AE,
∴当BG取得最大值时,AE取得最大值.
如图3,当旋转角为270°时,BG=AE.
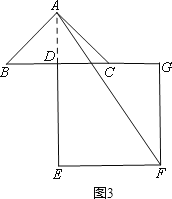
∵BC=DE=4,
∴BG=2+4=6.
∴AE=6.
在Rt△AEF中,由勾股定理,得
AF=![]() =
=![]() ,
,
∴AF=2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=x2-(2m-1)x-6m与x轴交于(x1,0)和(x2,0)两点,已知x1x2=x1+x2+49,要使此抛物线经过原点,应将它向右平移__________个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,这三种可能性大小相同,现在两辆汽车经过这个十字路口.
(1)请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果;
(2)求这两辆汽车都向左转的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
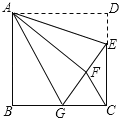
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() 为
为![]() 中点,
中点, ![]() 、
、![]() 与射线
与射线![]() 分别相交于点
分别相交于点![]() 、
、![]() (射线
(射线![]() 不经过点
不经过点![]() ).
).
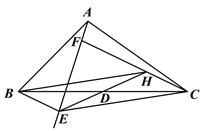
(1)如图①,当BE∥CF时,连接ED并延长交CF于点H. 求证:四边形BECH是平行四形;
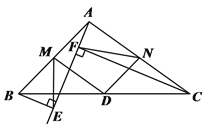
(2)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND. 求证:AM=AN
(3)如图②,当BE⊥AE于点E,CF⊥AE于点F时,分别取AB、AC的中点M、N,连接ME、MD、NF、ND. 求证:∠EMD=∠FND.
图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件: ①蜡烛在没有氧气的瓶中燃烧: ②掷一枚普通的骰子,朝上一面的点数不超过6: ③掷两枚质地均匀的正方体骰子,朝上一面的点数之和大于6④两个非零实数的积为正数.属于确定事件的个数是( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com