【题目】如图，已知∠1和∠2互为补角，∠A=∠D，求证：∠B=∠C．
请在下面的证明过程的括号内，填写依据．
证明：∵∠1与∠CGD是对顶角，
∴∠1=∠CGD（ ）
∵∠1+∠2=180°（已知）
∴∠2+∠CGD=180°（等量代换）
∴AE//FD（ ）
∴∠AEC=∠D（ ）
∵∠A=∠D（已知）
∴∠AEC=∠A（ ）
∴AB//CD（ ）
∴∠B=∠C（ ）
文敬图书课时先锋系列答案科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，一次函数y＝﹣
x+b的图象与y轴交于点B（0，2），与反比例函数y＝
的图象交于点A（4，﹣1）．
（1）求反比例函数的表达式和一次函数表达式；
（2）如果点P是x轴上的一点，且△ABP的面积是3，求P点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为4的正方形ABCD中，对角线AC，BD相交于点O，点E是AD边上一点，连接CE，把△CDE沿CE翻折，得到△CPE，EP交AC于点F，CP交BD于点G，连接PO，若PO∥BC，则四边形OFPG的面积是 ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB∥CD，分别探讨下面三个图形中∠AEC与∠EAB，∠ECD之间的关系，请你从所得到的关系中任选一个加以证明．
（1）在图1中，∠AEC与∠EAB，∠ECD之间的关系是：________________．
（2）在图2中，∠AEC与∠EAB，∠ECD之间的关系是：________________．
（3）在图3中，∠AEC与∠EAB，∠ECD之间的关系是：________________．
（4）在图______中，求证：________________．（并写出完整的证明过程）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从﹣4，﹣3，﹣2，﹣1，0，1，3，4，5这九个数中，随机抽取一个数，记为a，则数a使关于x的不等式组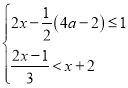
至少有四个整数解，且关于x的分式方程
＝1有非负整数解的概率是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将放在每个小正方形的边长为1的网格中，点A，B，C均落在格点上．
（1）计算AB边的长等于；
（2）在如图所示的网格中，用无刻度的直尺，画出一个以AB为一边的矩形，使矩形的面积等于△ABC的面积，并简要说明画图的方法（不要求证明）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：
材料1：对于一个关于
的二次三项式
，除了可以利用配方法求该多项式的取值范围外，爱思考的小川同学还想到了其他的方法；比如先令
，然后移项可得：
，再利用一元二次方程根的判别式来确定
的取值范围，请仔细阅读下面的例子：
例：求
的取值范围；
解：令
；
材料2：在学习完一元二次方程的解法后，爱思考的小川同学又想到仿造一元二次方程的解法来解决一元二次不等式的解集问题，他的具体做法如下：
若关于的一元二次方程
有两个不相等的实数根
、
，则关于的一元二次不等式
的解集为：
或
；则关于的一元二次不等式的
的解集为：
．
材料3：若关于的一元二次方程
有两个不相等的实数根、
；则
；
，我们称之为韦达定理；
请根据上述材料，解答下列问题：
（1）若关于的二次三项式
（
为常数）的最小值为
，则
________．
（2）求出代数式
的取值范围．
（3）若关于的代数式
（其中、
为常数，且
）的最小值为
，最大值为4，请求出满足条件的、的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
