
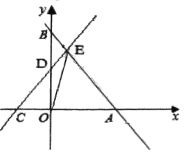
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,
,![]() 的解析式为
的解析式为![]() ,
,![]() 的解析式为
的解析式为![]() 且
且![]() ,两直线的交点
,两直线的交点![]() 。
。

(1)求直线![]() 的解析式;
的解析式;
(2)求四边形![]() 的面积;
的面积;
(3)当![]() 时,直接写出
时,直接写出![]() 的取值范围。
的取值范围。
【答案】(1)![]() ;(2)108;(3)x<3
;(2)108;(3)x<3
【解析】
(1)分别求出点A,B,E的坐标,利用![]() 求出点C的坐标,然后利用待定系数法求直线CD的解析式;(2)求出点D坐标,然后利用四边形
求出点C的坐标,然后利用待定系数法求直线CD的解析式;(2)求出点D坐标,然后利用四边形![]() 等于△DOE与△AOE的面积之和,即可求解;(3)结合图像,根据点E的坐标确定不等式的解集.
等于△DOE与△AOE的面积之和,即可求解;(3)结合图像,根据点E的坐标确定不等式的解集.
解:(1)在![]() 中
中
当x=0时,y=16
当y=0时,![]()
解得:![]()
∴点A(12,0);点B(0,16)
将点![]() 代入
代入![]() 中
中
![]()
∴点![]()
又∵![]()
∴点C(-6,0)
将点C,E代入直线CD的解析式为![]() 得:
得:![]()
解得:![]()
∴直线CD的解析式为![]()
(2)在![]() 中
中
当x=0时,y=8
∴点D的坐标为(0,8)
∴四边形![]() 的面积=S△DOE+S△AOE
的面积=S△DOE+S△AOE
∴![]()
(3)∵两直线的交点![]()
∴结合图像可得,![]() 的解集为:x<3
的解集为:x<3


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
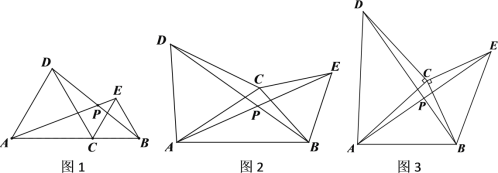
【题目】如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P
(1)观察猜想:①线段AE与BD的数量关系为_________;②∠APC的度数为_______________
(2)数学思考:如图2,当点C在线段AB外时,(1)中的结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明
(3)拓展应用:如图3,分别以AC、BC为边在AB同侧作等腰直角三角形ACD和等腰直角三角形BCE,其中∠ACD=∠BCE=90°,CA=CD,CB=CE,连接AE=BD交于点P,则线段AE与BD的关系为________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有个点![]() ,点
,点![]() 第1次向上跳动1个单位至点
第1次向上跳动1个单位至点![]() ,紧接着第2次向右跳动2个单位至点
,紧接着第2次向右跳动2个单位至点![]() ,第3次向上跳动1个单位,第4次向左跳动3个单位,第5次又向上跳动1个单位,第6次向右跳动4个单位,…,依次规律跳动下去,点
,第3次向上跳动1个单位,第4次向左跳动3个单位,第5次又向上跳动1个单位,第6次向右跳动4个单位,…,依次规律跳动下去,点![]() 第2019次跳动至点
第2019次跳动至点![]() 的坐标是( )
的坐标是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
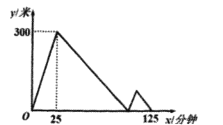
【题目】“龟、蟹赛跑趣事”:某天,乌龟和螃蟹在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑500米。当螃蟹领先乌龟300米时,螃蟹停下来休息并睡着了,当乌龟追上螃蟹的瞬间,螃蟹惊醒了(惊醒时间忽略不计)并立即以原来的速度继续跑向终点,并赢得了比赛。在比赛的整个过程中,乌龟和螃蟹的距离![]() (米)与乌龟出发的时间
(米)与乌龟出发的时间![]() (分钟)之间的关系如图所示,则螃蟹到达终点时,乌龟距终点的距离是______________米。
(分钟)之间的关系如图所示,则螃蟹到达终点时,乌龟距终点的距离是______________米。
查看答案和解析>>
科目:初中数学 来源: 题型:
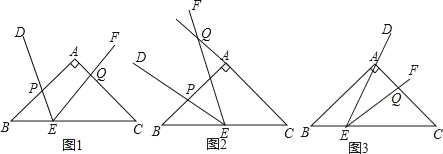
【题目】如图1,在等腰直角△ABC中,∠BAC=90°,AB=AC=2,点E是BC边上一点,∠DEF=45°且角的两边分别与边AB,射线CA交于点P,Q.
(1)如图2,若点E为BC中点,将∠DEF绕着点E逆时针旋转,DE与边AB交于点P,EF与CA的延长线交于点Q.设BP为x,CQ为y,试求y与x的函数关系式,并写出自变量x的取值范围;
(2)如图3,点E在边BC上沿B到C的方向运动(不与B,C重合),且DE始终经过点A,EF与边AC交于Q点.探究:在∠DEF运动过程中,△AEQ能否构成等腰三角形,若能,求出BE的长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)在长方形ABCD中,AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以1cm/s的速度移动,与此同时,点Q从点C开始沿边CB向终点B以2cm/s的速度移动,如果P、Q分别从A、C同时出发,当点Q运动到点B时,两点停止运动.设运动时间为t秒.

(1)填空:BQ=______________cm,PB=_______________cm(用含t的代数式表示);
(2)当t为何值时,PQ的长度等于![]() cm?
cm?
(3)是否存在t的值,使得五边形APQCD的面积等于27![]() ?若存在,请求出此时t的值;若不存在,请说明理由
?若存在,请求出此时t的值;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形中有大小不同的平行四边形,第一幅图中有1个平行四边形,第二幅图中有3个平行四边形,第三幅图中有5个平行四边形,则第6幅和第7幅图中合计有( )个平行四边形
![]()
A.22B.24C.26D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
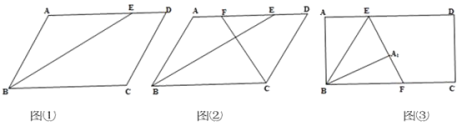
【题目】如图,城南中学八年级学习小组发现:当角平分线遇上平行线会出现等腰三角形。例如:图①,在四边形ABCD中,BE平分∠ABC,AD//BC,易得△ABE是等腰三角形。该小组将此结论作拓展:如图②,四边形ABCD中, BE平分∠BCD,CF平分∠ABC ,AD//BC,AB=CD=3,AD=4,则EF=________。如图③,如图,在长方形ABCD中,AB=3,BC=5,点E在边AD上,连接BE,△EAB沿BE翻折得到△EA1B,延长交BC于点F,若四边形EFCD的周长为11,则EF=________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com