
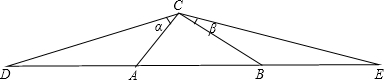
分析 延长CB,使BM=BC,通过△ABC≌△EBM,得到∠M=∠ACB=90°,AC=EM,于是求得cotβ=$\frac{CM}{EM}$=$\frac{2BC}{AC}$,同理cotα=$\frac{2AC}{BC}$,即可得到结论.
解答  解:延长CB,使BM=BC,
解:延长CB,使BM=BC,
在△ABC与△EBM中,
$\left\{\begin{array}{l}{BC=BM}\\{∠ABC=∠EBM}\\{AB=EB}\end{array}\right.$,
∴△ABC≌△EBM,
∴∠M=∠ACB=90°,AC=EM,
∴cotβ=$\frac{CM}{EM}$=$\frac{2BC}{AC}$,
同理cotα=$\frac{2AC}{BC}$,
∴cotα•cotβ=4.
点评 本题考查了解直角三角形,全等三角形的判定和性质,正确的作出辅助线是解题的关键.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2=b2+c2+2bccosA | B. | a2=b2+c2+bccosA | ||
| C. | a2=b2+c2-2bccosA | D. | a2=b2+c2-2bcsinA |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
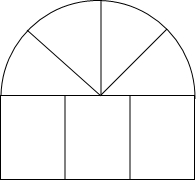 从房屋的窗户的形状如图所示,它的上部是四个小扇形组成的半圆,下部是有三个相同的小矩形组成,制作窗框的材料总长为15m,设半圆的半径为xm,窗户的截面面积为Sm2.
从房屋的窗户的形状如图所示,它的上部是四个小扇形组成的半圆,下部是有三个相同的小矩形组成,制作窗框的材料总长为15m,设半圆的半径为xm,窗户的截面面积为Sm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+1)(a-1) | B. | (2+a)(a+2) | C. | (-a+b)(-a+b) | D. | (a2-b)(a-b2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
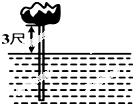 如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面3尺.突然一阵大风吹过,红莲被吹至一边,花朵刚好齐及水面,如果知道红莲移动的水平距离为6尺,则水是( )尺.
如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面3尺.突然一阵大风吹过,红莲被吹至一边,花朵刚好齐及水面,如果知道红莲移动的水平距离为6尺,则水是( )尺.| A. | 3.5 | B. | 4 | C. | 4.5 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com