下面给出两个判断:
(1)有两边和第三边上的中线对应相等的两个三角形全等;
(2)在三角形6个边、角元素中,有5个元素分别相等的两个三角形全等.
上述判断是否正确?若正确,请给出证明过程;若不正确,请说明理由.
解:(1)正确.
如图所示,在△ABC与△A′B′C′中,AB=A′B′,AC=A′C′,AD•A′D′分别为BC、B′C′
上的中线,且AD=A′D′,
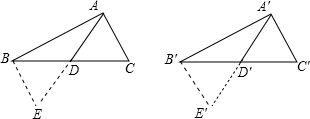
.
求证:△ABC≌△A′B′C′.
证明:∵D、D′分别为BC、B′C′的中点,把△ACD和A′C′D′分别绕D、D′点按顺时针旋转180°可得到△ABE与△A′B′E′,
∴AB=A′B′,BE=B′E′,AE=A′E′,
∴△ABE≌△A′B′E′,
∴∠BAE=∠B′A′E′,
同理可得∠CAD=∠C′A′D′,
∴∠BAC=∠B′A′C′,
∴△ABC≌△A′B′C′.
(2)不正确.
如三边长分别为8,12,18和12,18,27的两个三角形,
其三边对应成比例,则这两个三角形相似,且有5个元素相等,
但它们对应边不相等,所以不全等.
分析:(1)根据题目要求画出图形,如图所示,根据已知条件利用SSS求证△ABE≌△A'B'E',得出∠BAE=∠B'A'E',同理可得∠CAD=∠C'A'D',然后可得∠BAC=∠B'A'C',再利用SAS即可证明△ABC≌△A'B'C'.
(2)例如两个三角形三边长分别为8,12,18和12,18,27的两个三角形显然相拟,根据全等三角形的判定但它们不全等.
点评:此题主要考查学生对全等三角形的判定这一知识点的理解和掌握,解答此题的关键是熟练掌握全等三角形的判定定理.

 .
.

 与
与 ,
, 与
与 .
.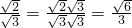 .
.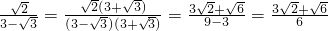 .
.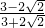 ;②
;②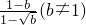 ;
;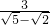 时,甲的解法是:
时,甲的解法是: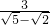 =
= =
=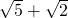 ,乙的解法是:
,乙的解法是: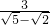 =
=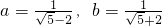 =
=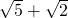 ,以下判断正确的是
,以下判断正确的是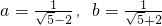 ,则
,则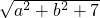 的值为
的值为