
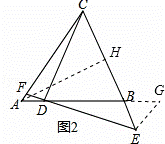
��ͼ1����ABC�У�AB=AC����D��BA���ӳ����ϣ���E��BC�ϣ�DE=DC����F��DE��AC�Ľ��㣬��DF =FE��
=FE��
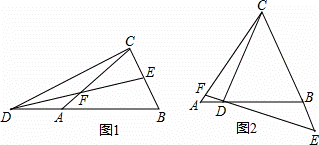
��1��ͼ1���Ƿ�������BDE��ȵĽǣ������ڣ����ҳ���������֤�����������ڣ�˵�����ɣ�
��2����֤��BE=EC��
��3����������D��BA���ӳ����ϣ���E��BC�ϡ��͡���F��DE��AC�Ľ��㣬��DF=FE���ֱ��Ϊ����D��AB�ϣ���E��CB���ӳ����ϡ��͡���F��ED���ӳ�����AC�Ľ��㣬��DF=kFE���������������䣨��ͼ2������AB=1����ABC=aʱ����BE�ij����ú�k��a��ʽ�ӱ�ʾ����
�⣺��1����DCA=��BDE��
֤������AB=AC��DC=DE��
���ABC=��ACB����DEC=��DCE��
���BDE=��DEC����DBC=��DCE����ACB=��DCA��
��2������E��EG��AC����AB�ڵ�G����ͼ1��
����DAC=��DGE��
�ڡ�DCA�͡�EDG�У�
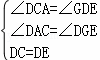
���DCA�ա�EDG��AAS����
��DA=EG��CA=DG��
 ��DG=AB��
��DG=AB��
��DA=BG��
��AF��EG��DF=EF��
��DA=AG��
��AG=BG��
��EG��AC��
��BE=EC��
��3������E��EG��AC����AB���ӳ����ڵ�G����ͼ2��
��AB=AC��DC=DE��
���ABC=��ACB����DEC=��DCE��
���BDE=��DBC����DEC=��ACB����DCE=��DCA��
��AC��EG��
���DAC=��DGE��
�ڡ�DCA�͡�EDG�У�

���DCA�ա�EDG��AAS����
��DA=EG��CA=DG
��DG=AB=1��
��AF��EG��
���ADF�ס�GDE��
�� ��
��
��DF=kFE��
��DE=EF��DF=��1��k��EF��
�� ��
��
��AD= ��
��
��GE=AD= ��
��
����A��AH��BC������ΪH����ͼ2��
��AB=AC��AH��BC��
��BH=CH��
��BC=2BH��
��AB=1����ABC=����
��BH=AB•cos��ABH=cos����
��BC=2cos����
��AC��EG��
���ABC�ס�GBE��
��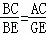 ��
��
��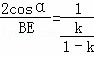 ��
��
��BE= ��
��
��BE�ij�Ϊ ��
��



 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��A��B��C��D�ĸ�����ڡ�O�ϣ���AOD=70�㣬AO��DC�����B�Ķ���Ϊ��������
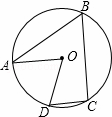
| �� | A�� | 40�� | B�� | 45�� | C�� | 50�� | D�� | 55�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
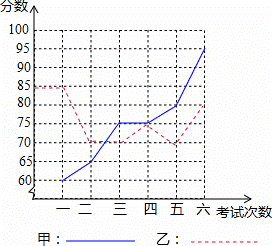
�ס�������ͬѧ������ĺ�ij��6�ο��Գɼ���ͼ��
��1���������ͼ��д�����
| ƽ���� | ���� | ��λ�� | ���� | ���� | |
| �� | 75 | �� �� | 75 | �� �� | �� �� |
| �� | �� �� | 33.3 | �� �� | �� �� | 15 |
��2������ֱ������������ͬ�ķ���Լס�������ͬѧ6�ο��Գɼ����з�����
�ٴ�ƽ�����ͷ������Ͽ����ڴ�����ͼ������ͬѧ�����������Ͽ�������Ϊ��ӳ��ʲô���⣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
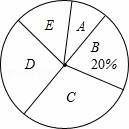
ij��Ϊ�˽����±仯�������ij������12ʱ�����£���λ���棩������ͳ�ƣ�����Ǹ����й�����������ͳ��ͼ����һ���֣�
| ���� | ����x | ���� |
| A | 4��x��8 | a |
| B | 8��x��12 | 6 |
| C | 12��x��16 | 9 |
| D | 16��x��20 | 8 |
| E | 20��x��24 | 4 |
����������Ϣ����������⣺
��1�����������12ʱ��������8����12�棨����12�棩������Ϊ��6���죬ռ������������İٷֱ�Ϊ�� ��%������¹����� ���죻
��2��ͳ�Ʊ��е�a=���������������12ʱ���������� ����Χ�ڵ�������ࣻ
��3�������������12ʱ�����²�����16�������ռ�����������İٷֱȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
һ��������ı���չ��ͼ��ͼ��ʾ���������ϸ���һ�֣�����������˼�ǡ�Ԥף�п��ɹ����������۳���������롰�ɡ���Ե����ǣ�������

| �� | A�� | �� | B�� | �� | C�� | �� | D�� | ף |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij�̳������±ʴ����۵��������ͳ�����±���ʾ��
| ��ɫ | ��ɫ | ��ɫ | ��ɫ | ��ɫ | ��ɫ |
| ���������� | 56 | 128 | 520 | 210 | 16 |
�����������½��ʴ�ʱ���һЩ��ɫ�ģ���������һ����Ӧ�����ĸ�ͳ��֪ʶ��������
| �� | A�� | ƽ���� | B�� | ���� | C�� | ��λ�� | D�� | ���� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com