
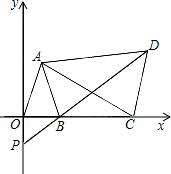
 如图,平面直角坐标系中,已知点A(a-b,a+b),B(a,0),且$\sqrt{a-b-3}$+(a-2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
如图,平面直角坐标系中,已知点A(a-b,a+b),B(a,0),且$\sqrt{a-b-3}$+(a-2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.分析 (1)先根据非负数的性质求出a、b的值,作AE⊥OB于点E,由SAS定理得出△AEO≌△AEB,根据全等三角形的性质即可得出结论;
(2)先根据∠CAD=∠OAB,得出∠OAC=∠BAD,再由SAS定理即可得出△AEO≌△AEB;
(3)设∠AOB=∠ABO=α,由全等三角形的性质可得出∠ABD=∠AOB=α,故∠OBP=180°-∠ABO-∠ABD=180°-2α为定值,再由OB=2,∠POB=90°可知OP的长度不变,故可得出结论.
解答 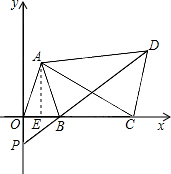 (1)证明:∵$\sqrt{a-b-3}$+(a-2b)2=0,
(1)证明:∵$\sqrt{a-b-3}$+(a-2b)2=0,
∴$\left\{\begin{array}{l}{a-b-3=0}\\{a-2b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=6}\\{b=3}\end{array}\right.$,
∴A(3,9),B(6,0),
作AE⊥OB于点E,
∵A(3,9),B(6,0),
∴OE=3,BE=6-3=3,
在△AEO与△AEB中,
∵$\left\{\begin{array}{l}{AE=AE}\\{∠AEO=∠AEB=90°}\\{OE=BE}\end{array}\right.$,
∴△AEO≌△AEB,
∴AO=AB;
(2)证明:∵∠CAD=∠OAB,
∴∠CAD+∠BAC=∠OAB+∠BAC,即∠OAC=∠BAD,
在△AOC与△ABD中,
∵$\left\{\begin{array}{l}{OA=AB}\\{∠OAC=∠BAD}\\{AC=AD}\end{array}\right.$,
∴△AOC≌△ABD(SAS);
(3)解:点P在y轴上的位置不发生改变.
理由:设∠AOB=∠ABO=α,
∵由(2)知,△AOC≌△ABD,
∴∠ABD=∠AOB=α,
∵OB=2,∠OBP=180°-∠ABO-∠ABD=180°-2α为定值,∠POB=90°,
∴OP长度不变,
∴点P在y轴上的位置不发生改变.
点评 本题考查的是全等三角形的判定与性质,熟知全等三角形的判定定理是解答此题的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
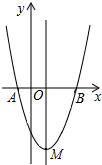 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,在长为16m,宽为10m的矩形耕地上,修筑同样宽的三条道路(互相垂直),把耕地分成六块试验田,要使试验田总面积为114m2,道路应为多宽?设道路宽x m,那么x满足方程( )
如图所示,在长为16m,宽为10m的矩形耕地上,修筑同样宽的三条道路(互相垂直),把耕地分成六块试验田,要使试验田总面积为114m2,道路应为多宽?设道路宽x m,那么x满足方程( )| A. | (10-x)(16-2x)=114 | B. | 160-(10+32)x=114 | ||
| C. | (10-2x)(16-x)=114 | D. | 114+(10+32)x+2x2=160 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
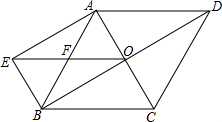 如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 假如小猫在如图所示的地板(图中每块方砖面积相等,小猫只停留在一块方砖上)上自由走动,它最终没有停在白色方砖上的概率为( )
假如小猫在如图所示的地板(图中每块方砖面积相等,小猫只停留在一块方砖上)上自由走动,它最终没有停在白色方砖上的概率为( )| A. | $\frac{5}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{9}$ | D. | $\frac{6}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com