
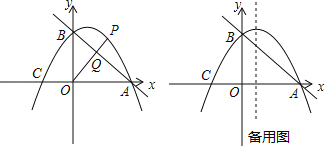
����Ŀ����ͼ��ֱ��y=��![]() x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=��
x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=��![]() x2+bx+c����A��B���㣬��x�����һ������ΪC��
x2+bx+c����A��B���㣬��x�����һ������ΪC��
��1���������ߵĽ���ʽ��
��2����P�ǵ�һ�����������ϵĵ㣬����OP��ֱ��AB�ڵ�Q�����P�ĺ�����Ϊm��PQ��OQ�ı�ֵΪy����y��m�Ĺ�ϵʽ�������PQ��OQ�ı�ֵ�����ֵ��
��3����D�������߶Գ����ϵ�һ���㣬����OD��CD������ODC���Բ��Բ��ΪM����sin��ODC��ֵ���ʱ�����M�����꣮
���𰸡���1�������߽���ʽΪy=��![]() x2+
x2+![]() x+3����2��y=��
x+3����2��y=��![]() m2+
m2+![]() m��PQ��OQ�ı�ֵ�����ֵΪ
m��PQ��OQ�ı�ֵ�����ֵΪ![]() ����3����M������Ϊ����1��
����3����M����������1��![]() ����1����
����1����![]() ����
����
��������
��1������ֱ�߽���ʽ��õ�A��B�����꣬�������������������߽���ʽ���ɵã�
��2������P��y���ƽ���߽�AB�ڵ�E���ݴ�֪��PEQ�ס�OBQ�����ݶ�Ӧ�߳ɱ�����y=![]() PE����P��m����
PE����P��m����![]() m2+
m2+![]() m+3����E��m����
m+3����E��m����![]() m+3����PE=��
m+3����PE=��![]() m2+
m2+![]() m�����y=
m�����y=![]() PE�ɵú�������ʽ�����ö��κ������ʵ������ֵ��
PE�ɵú�������ʽ�����ö��κ������ʵ������ֵ��
��3����CO�Ĵ�ֱƽ������CO���ڵ�N��֪��M��CO�Ĵ�ֱƽ�����ϣ�����OM��CM��DM�����ݡ�ODC=![]() ��CMO=��OMN��MC=MO=MD֪sin��ODC=sin��OMN=
��CMO=��OMN��MC=MO=MD֪sin��ODC=sin��OMN=![]() ����MDȡ��Сֵʱ��sin��ODC��ݴ˽�һ�����ɵã�
����MDȡ��Сֵʱ��sin��ODC��ݴ˽�һ�����ɵã�
��1����y=��![]() x+3����y=0��x=4����x=0��y=3��
x+3����y=0��x=4����x=0��y=3��
���A��4��0����B��0��3����
��A��4��0����B��0��3������y=��![]() x2+bx+c���ã�
x2+bx+c���ã�
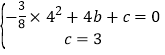 ��
��
��ã�![]() ��
��
�������߽���ʽΪy=��![]() x2+
x2+![]() x+3��
x+3��
��2����ͼ1������P��y���ƽ���߽�AB�ڵ�E��
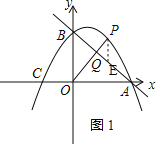
����PEQ�ס�OBQ��
��![]() ��
��
��![]() =y��OB=3��
=y��OB=3��
��y=![]() PE��
PE��
��P��m����![]() m2+
m2+![]() m+3����E��m����
m+3����E��m����![]() m+3����
m+3����
��PE=����![]() m2+
m2+![]() m+3��������
m+3��������![]() m+3��=��
m+3��=��![]() m2+
m2+![]() m��
m��
��y=![]() ����
����![]() m2+
m2+![]() m��=��
m��=��![]() m2+
m2+![]() m=��
m=��![]() ��m��2��2+
��m��2��2+![]() ��
��
��0��m��3��
�൱m=2ʱ��y���ֵ=![]() ��
��
��PQ��OQ�ı�ֵ�����ֵΪ![]() ��
��
��3����ͼ����������y=��![]() x2+
x2+![]() x+3����C����2��0�����Գ���Ϊֱ��x=1��
x+3����C����2��0�����Գ���Ϊֱ��x=1��
�ߡ�ODC������Ϊ��M��
���M��CO�Ĵ�ֱƽ�����ϣ�
��CO�Ĵ�ֱƽ������CO���ڵ�N������OM��CM��DM��
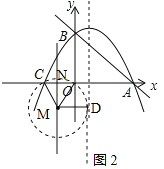
���ODC=![]() ��CMO=��OMN��MC=MO=MD��
��CMO=��OMN��MC=MO=MD��
��sin��ODC=sin��OMN=![]() ��
��
��MO=MD��
�൱MDȡ��Сֵʱ��sin��ODC���
��ʱ��M��ֱ��x=1���У�MD=2��
MN=![]() =
=![]() ��
��
���M����1����![]() ����
����
���ݶԳ��ԣ���һ�㣨��1��![]() ��Ҳ�������⣻
��Ҳ�������⣻
������������M����������1��![]() ����1����
����1����![]() ����
����


 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,![]() ��
��![]() ���������н��ۣ���
���������н��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ��
��![]() ��������ȷ���ǣ� ��
��������ȷ���ǣ� ��
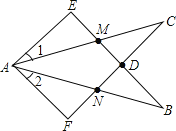
A. �٢ۢܣ�B. �ڢۢܣ�C. �٢ڢ�D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ�ߺ�Բ�滭һ���ǵ�����֪��������������ȫ�������εĶ�Ӧ���������һ��������ȫ�ȵ��������� ��

A��SAS B��ASA C��AAS D��SSS
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�������������ȱˮ�Ĺ���֮һ��Ϊ����ǿ����Ľ�ˮ��ʶ��ij����ˮ��˾�Ծ�����ˮ��ȡ�Ի�Ϊ��λ�ֶμƷѰ취�շѣ���ÿ����ˮ10�����ڣ�����10�֣����û���ÿ��ˮ�շ�aԪ��ÿ����ˮ����10�ֵIJ��֣���ÿ��bԪ��b��a���շѣ���һ����������ˮx���֣���Ӧ��ˮ��y��Ԫ����y��x֮��ĺ�����ϵ��ͼ��ʾ.
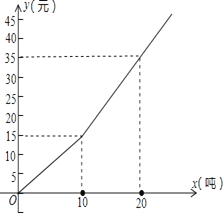
��1���ֶ�д��y��x�ĺ�����ϵʽ.
��2��ij������������ˮ8�֣�Ӧ��ˮ�Ѷ���Ԫ��
��3����֪��������±Ⱦ����Ҷ���ˮ4�֣�����һ����ˮ��46Ԫ�����������·ֱ���ˮ���ٶ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һԪ���η���2x2+2x��1=0��������Ϊx1��x2����x1��x2�����н�����ȷ���ǣ�������
A. x1+x2=1 B. x1x2=��1 C. |x1|��|x2| D. x12+x1=![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���B������Ϊ��4��2����ֱ��y=��![]() x+
x+![]() ���AB��BC�ֱ��ཻ�ڵ�M��N������y=
���AB��BC�ֱ��ཻ�ڵ�M��N������y=![]() ��x��0����ͼ�����M��
��x��0����ͼ�����M��
��1����˵����NҲ�ں���y=![]() ��x��0����ͼ���ϣ�
��x��0����ͼ���ϣ�
��2����ֱ��MN��y��ĸ�����ƽ�Ƶõ�ֱ��M��N�䣬��ֱ��M��N���뺯��y�T![]() ��x��0����ͼ�����һ������ʱ����ֱ��M'N��Ľ���ʽ��
��x��0����ͼ�����һ������ʱ����ֱ��M'N��Ľ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ҳ�����ѧ����У���ֻ�������Ŀ�����ijУ�����꼶��ȤС������������˸�Уѧ���ҳ������������Ե����������������������²�������ͳ��ͼ��
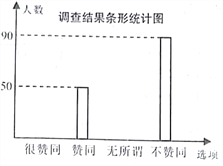
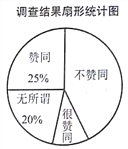
�����������Ϣ�������������
(1)��ν��ܵ���ļҳ�������Ϊ________�ˣ�
(2)������ͳ��ͼ������������ͬ������Ӧ������Բ�ĽǵĶ�����
(3)������ν��ܵ���ļҳ�����������һ���ҳ���ǡ�ó鵽������ν���ļҳ������Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
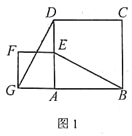
����Ŀ����ͼ1��������ABCD��������AEFG������DG��BE��
(1)����
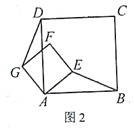
��������AEFG�Ƶ�A��ת����ͼ2�����߶�DG��BE֮���������ϵ��____________����ֱ��DG��ֱ��BE֮���λ�ù�ϵ��____________��
(2)̽��
��ͼ3�����ı���ABCD���ı���AEFG��Ϊ��������AD=2AB��AG=2AE��֤����ֱ��DG��BE
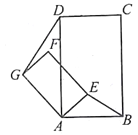
(3)Ӧ��
��(2)�����������GE(��E��AB�Ϸ�)����GE��AB����AB=![]() ��AE=1�����߶�DG�Ƕ���?(ֱ��д������)
��AE=1�����߶�DG�Ƕ���?(ֱ��д������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ y��![]() ��ͼ����һ�κ���y��mx��b��ͼ��������A��1,3��,B��n,��1����
��ͼ����һ�κ���y��mx��b��ͼ��������A��1,3��,B��n,��1����
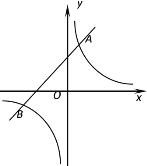
��1������������һ�κ����ĺ�����ϵʽ��
��2������ͼ��ֱ�ӻش𣺵�xȡ��ֵʱ��һ�κ�����ֵ���ڷ�����������ֵ��
��3������AO��BO������ABO�������
��4����y���ϴ��ڵ�P��ʹ��AOPΪ���������Σ���ֱ��д����P������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com