Question

17．如图1，在平面直角坐标系中，直线l交x轴、y轴分别于A、B两点，A（a，0），B（0，b），且满足-$\sqrt{b-4}$-a²+2ab-b²=0．
（1）求A、B的坐标；
（2）如图1，C是线段AB上一点，C点的横坐标为1，P为y轴上一点，且满足∠OCP=45°，求P点坐标；
（3）如图2，过点B作BD⊥OC，分别交OC、OA的延长线于F、D两点，E为AO延长线上一点，且∠CEA=∠BDO，求证：OE=AD．

Answer 1

分析 （1）根据二次根式和平方的非负性列式得出a、b的值，写出点A、B的坐标；
（2）如图1，设P（0，y），先求直线AB的解析式，并求出点C的坐标；利用勾股定理计算OC的长，再根据面积法列等量关系式，求出y的值，当y=5时，不符合∠OCP=45°，所以y=$\frac{5}{2}$，写出点P的坐标；
（3）如图2，作辅助线，构建直角三角形，利用面积法求出BF的长，再利用勾股定理求OF，证明根据△BOF∽△BDO和△CME∽△BOD，根据相似比分别求出AD和OE的值，得出结论．

解答 解：（1）∵点A（a，0），B（0，b），满足-$\sqrt{b-4}$-a²+2ab-b²=0，
∴（$\sqrt{b-4}$）+（a²-2ab+b²）=0，
∴$\sqrt{b-4}$+（a-b）²=0，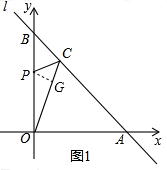
∴a=b=4，
∴A（4，0），B（0，4）
（2）如图1，设P（0，y），过p作PG⊥OD于G，
设直线AB的解析式为：y=kx+b，
把A（4，0），B（0，4）代入得：$\left\{\begin{array}{l}{4k+b=0}\\{b=4}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$，
∴直线AB的解析式为：y=-x+4，
∵C是线段AB上一点，C点的横坐标为1，
∴当x=1时，y=3，
则C（1，3），
∴OC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$，
∵∠OCP=45°，
∴△PCG是等腰直角三角形，
∴PG=CG，PG=$\frac{\sqrt{2}}{2}$PC，
PC=$\sqrt{（0-1）^{2}+（y-3）^{2}}$=$\sqrt{1+（y-3）^{2}}$，
∵S_△POC=$\frac{1}{2}$OP×1=$\frac{1}{2}$OC•PG，
∴OP=OC•PG，
则y=$\sqrt{10}$×$\frac{\sqrt{2}}{2}$×$\sqrt{1+（y-3）^{2}}$，
解得：y₁=5（舍），y₂=$\frac{5}{2}$，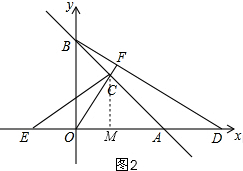
∴P（0，$\frac{5}{2}$）；
（3）如图2，过C作CM⊥OA，垂足为M，则CM=3，
∵△AOB为等腰三角形，
∴∠BAO=45°，
∴AM=CM=3，
∵BD⊥OC，
∵S_△BOC=$\frac{1}{2}$OC•BF=$\frac{1}{2}$OB×1，
∴OC•BF=OB，
$\sqrt{10}$×BF=4，
∴BF=$\frac{2\sqrt{10}}{5}$，
在Rt△BOF中，OF=$\sqrt{O{B}^{2}-B{F}^{2}}$=$\sqrt{{4}^{2}-（\frac{2\sqrt{10}}{5}）^{2}}$=$\frac{6\sqrt{10}}{5}$，
∵∠OBF=∠OBD，∠BOD=∠BFO=90°，
∴△BOF∽△BDO，
∴$\frac{OF}{BF}=\frac{OD}{BO}$，
∴$\frac{OD}{BO}=\frac{\frac{6\sqrt{10}}{5}}{\frac{2\sqrt{10}}{5}}$=3，
∴OD=3OB=3×4=12，
∴AD=12-4=8，
∵∠CEA=∠BDO，∠CME=∠BOD=90°，
∴△CME∽△BOD，
∴$\frac{CM}{BO}=\frac{ME}{OD}$，
∴$\frac{ME}{CM}=\frac{OD}{BO}$=3，
∴ME=3CM=3×3=9，
∴OE=ME-OM=9-1=8，
∴AD=OE．

点评 本题是三角形的综合题，并与坐标和一次函数相结合，考查了等腰直角三角形、相似三角形的判定和性质；同时要熟练掌握利用待定系数法求一次函数的解析式，并根据解析式求图象上某点的坐标，与几何图形相结合，写出边的长度，注意边为正值；本题还运用了面积法求线段的长．