
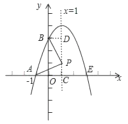
【题目】已知抛物线![]() 在坐标系中的位置如图所示,它与
在坐标系中的位置如图所示,它与![]() ,
,![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() ,
,![]() 是其对称轴
是其对称轴![]() 上的动点,根据图中提供的信息,给出以下结论:①
上的动点,根据图中提供的信息,给出以下结论:①![]() ,②
,②![]() 是
是![]() 的一个根,③若
的一个根,③若![]() ,
,![]() ,则
,则![]() .其中正确的有______个.
.其中正确的有______个.

【答案】3
【解析】
①根据对称轴方程即可得结论;②根据对称轴和抛物线与x轴的一个交点坐标即可求出另一个交点坐标即可得结论;③构造PA和PB所在直角三角形全等,得线段相等,从而求得B点的坐标,再根据交点式求抛物线解析式,求当x=1时,y的值即可得结论.
解:①因为抛物线的对称轴x=1,
所以![]() =1,即b+2a=0,
=1,即b+2a=0,
所以①正确;
②因为A(1,0),对称轴x=1,
所以设抛物线与x轴的另一个交点为E,
所以E(3,0),
所以x=3时,y=0,即x=3是ax2+bx+c=0的一个根.
所以②正确;
③如图:过点B作BD⊥对称轴于点D,设对称轴交x轴于点C,
∵AP⊥BP,
∴∠APB=90°,
∴∠APC+∠BPD=90°,
∵∠BPD+∠PBD=90°,
∴∠PBD=∠APC,
∵AP=BP,
∴Rt△APC≌Rt△PBD(AAS)
∴PC=BD=1,DP=AC=2,
∴DC=3,
∴OB=3,
∴B(0,3).又E(3,0),A(1,0).
设抛物线解析式为y=a(x+1)(x3),
把B(0,3)代入,解得a=1,
∴抛物线解析式为x2+2x+3,
当x=1时,y=4,
即a+b+c=4.
所以③正确.
故答案为3.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若P和Q两点关于原点对称,则称点P与点Q是一个“和谐点对”,表示为[P,Q],比如[P(1,2),Q(﹣1,﹣2)]是一个“和谐点对”.
(1)写出反比例函数y=![]() 图象上的一个“和谐点对”;
图象上的一个“和谐点对”;
(2)已知二次函数y=x2+mx+n,
①若此函数图象上存在一个和谐点对[A,B],其中点A的坐标为(2,4),求m,n的值;
②在①的条件下,在y轴上取一点M(0,b),当∠AMB为锐角时,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
A型利润(元/件) | B型利润(元/件) | |
甲店 | 180 | 150 |
乙店 | 120 | 110 |
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并写出x的取值范围;
(2)若要求总利润超过14960元,有多少种不同分配方案?请列出具体方案;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润,甲店的B型产品以及乙店的A,B型产品的每件利润不变,该公司如何设计分配方案,使总利润达到最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=4,D、E分别为射线CB、AC上的两动点,且BD=CE,直线AD和BE相交于M点,则CM的最大值为( )
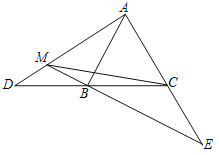
A.2![]() B.
B.![]() C.3
C.3![]() D.4
D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
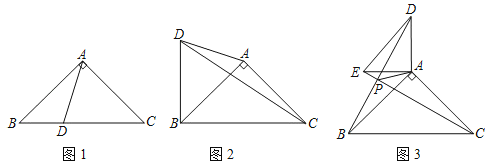
【题目】在△ABC中,AB=AC,∠BAC=90°,D为平面内的一点.
(1)如图1,当点D在边BC上时,且∠BAD=30°,求证:AD=![]() BD.
BD.
(2)如图2,当点D在△ABC的外部,且满足∠BDC﹣∠ADC=45°,求证:BD=![]() AD.
AD.
(3)如图3,若AB=4,当D、E分别为AB、AC的中点,把△DAE绕A点顺时针旋转,设旋转角为α(0<α≤180°),直线BD与CE的交点为P,连接PA,直接写出△PAC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坚持农业农村优先发展,按照产业兴旺、生态宜居的总要求,统筹推进农村经济建设.洛宁县某村出售特色水果(苹果).规定如下:
品种 | 购买数量低于50箱 | 购买数量不低于50箱 |
新红星 | 原价销售 | 以八折销售 |
红富士 | 原价销售 | 以九折销售 |
如果购买新红星40箱,红富士60箱,需付款4300元;如果购买新红星100箱,红富士35箱,需付款4950元.
(1)每箱新红星、红富士的单价各多少元?
(2)某单位需要购置这两种苹果120箱,其中红富士的数量不少于新红星的一半,并且不超过60箱,如何购买付款最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某坦克部队需要经过一个拱桥(如图所示),拱桥的轮廓是抛物线形,拱高OC=6m,跨度AB=20m,有5根支柱:AG、MN、CD、EF、BH,相邻两支柱的距离均为5m.

(1)以AB的中点为原点,AB所在直线为x轴,支柱CD所在直线为y轴,建立平面直角坐标系,求抛物线的解析式;
(2)若支柱每米造价为2万元,求5根支柱的总造价;
(3)拱桥下面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道是坦克的行进方向,现每辆坦克长4m,宽2m,高3m,行驶速度为24km/h,坦克允许并排行驶,坦克前后左右距离忽略不计,试问120辆该型号坦克从刚开始进入到全部通过这座长1000m的拱桥隧道所需最短时间为多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长度为_____

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com