
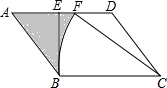
 如图,平行四边形ABCD中,BE⊥AD于点E,以C为圆心,BC长为半径画弧,恰好过AD的中点F,若BC=4,BE=2,则图中阴影部分的面积为6-$\frac{4}{3}$π.
如图,平行四边形ABCD中,BE⊥AD于点E,以C为圆心,BC长为半径画弧,恰好过AD的中点F,若BC=4,BE=2,则图中阴影部分的面积为6-$\frac{4}{3}$π. 分析 过F作FH⊥BC于H,推出四边形EFHB是矩形,得到FH=BE=2,根据直角三角形的性质到底∠BCF=30°,根据图形的面积公式即可得到结论.
解答 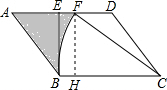 解:过F作FH⊥BC于H,
解:过F作FH⊥BC于H,
∵BE⊥AD,
∴四边形EFHB是矩形,
∴FH=BE=2,
∵CF=BC=4,
∴∠BCF=30°,
平行四边形ABCD中,∵AD=BC=4,AD∥BC,
∴AF=$\frac{1}{2}$AD=2,
∴S阴影=S四边形ABCF-S扇形=$\frac{1}{2}$(2+4)×2-$\frac{30•π×{4}^{2}}{360}$=6-$\frac{4}{3}$π,
故答案为:6-$\frac{4}{3}$π.
点评 本题考查的是扇形面积的计算,平行四边形的性质,熟记扇形的面积公式是解答此题的关键.


科目:初中数学 来源: 题型:解答题
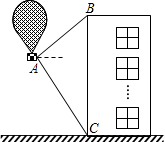 “五一”节期间在我市市民广场进行了热气球飞行表演,如图,有一热气球到达离地面高度为36米的A处时,仪器显示如图,有一热气球到达离地面高度为36米的A处时,仪器显正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)
“五一”节期间在我市市民广场进行了热气球飞行表演,如图,有一热气球到达离地面高度为36米的A处时,仪器显示如图,有一热气球到达离地面高度为36米的A处时,仪器显正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某一时刻太阳光从教室窗户射入室内,与地面的夹角∠BPC为30°,窗户的一部分在教室地面所形成的影长PE为3.5米,窗户的高度AF为2.5米.求窗外遮阳蓬外端一点D到教室窗户上椽的距离AD.(参考数据:$\sqrt{3}$≈1.7,结果精确0.1米)
如图,某一时刻太阳光从教室窗户射入室内,与地面的夹角∠BPC为30°,窗户的一部分在教室地面所形成的影长PE为3.5米,窗户的高度AF为2.5米.求窗外遮阳蓬外端一点D到教室窗户上椽的距离AD.(参考数据:$\sqrt{3}$≈1.7,结果精确0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{210}{x}$-1.8=$\frac{210}{1.5x}$ | B. | $\frac{210}{x}$+1.8=$\frac{210}{1.5x}$ | ||
| C. | $\frac{210}{x}$+1.5=$\frac{210}{1.8x}$ | D. | $\frac{210}{x}$-1.5=$\frac{210}{1.8x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
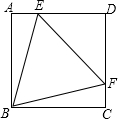 如图,正方形ABCD中,点E、F分别在AD、DC上,且△BEF为等边三角形.下列结论:①DE=DF;②∠AEB=75°;③AE+CF=EF;④BE=$\sqrt{2}$DE;⑤△EDF与△BFC的面积比为2:1.其中正确的结论有4个.
如图,正方形ABCD中,点E、F分别在AD、DC上,且△BEF为等边三角形.下列结论:①DE=DF;②∠AEB=75°;③AE+CF=EF;④BE=$\sqrt{2}$DE;⑤△EDF与△BFC的面积比为2:1.其中正确的结论有4个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
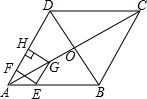 如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒
如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com