
分析 (1)根据完全平方公式,可得1+$\frac{1}{{n}^{2}}$+$\frac{1}{(n+1)^{2}}$=[1+($\frac{1}{n}$-$\frac{1}{1+n}$)]2,根据开方运算,可得$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(1+n)^{2}}}$=1+$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)根据$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(1+n)^{2}}}$=1+$\frac{1}{n}$-$\frac{1}{n+1}$,可化简二次根式,根据分式的加减运算,可得答案.
解答 解:(1)∵1+$\frac{1}{{n}^{2}}$+$\frac{1}{(n+1)^{2}}$=1+[$\frac{1}{n}$-$\frac{1}{(n+1)^{\;}}$]2+2$\frac{1}{n(n+1)}$
=1+2[$\frac{1}{n}$-$\frac{1}{n+1}$]+[$\frac{1}{n}$-($\frac{1}{1+n}$)]2
=[1+($\frac{1}{n}$-$\frac{1}{1+n}$)]2,
$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(1+n)^{2}}}$-1=1+$\frac{1}{n}$-$\frac{1}{n+1}$-1=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}+\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}+$…$+\sqrt{1+\frac{1}{{9}^{2}}+\frac{1}{1{0}^{2}}}$
=1+1-$\frac{1}{2}$+1+$\frac{1}{2}$-$\frac{1}{3}$+1+$\frac{1}{3}$-$\frac{1}{4}$+…1+$\frac{1}{9}$-$\frac{1}{10}$
=10-$\frac{1}{10}$
=9$\frac{9}{10}$.
点评 本题考查了二次根式的性质与化简,利用完全平方公式得出1+$\frac{1}{{n}^{2}}$+$\frac{1}{(n+1)^{2}}$=[1+($\frac{1}{n}$-$\frac{1}{1+n}$)]2是解题关键.


科目:初中数学 来源: 题型:解答题
 如图,一位驾驶员看到前方斑马线上有行人横穿马路,采取紧急刹车,汽车滑行12米距离后停下,
如图,一位驾驶员看到前方斑马线上有行人横穿马路,采取紧急刹车,汽车滑行12米距离后停下,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
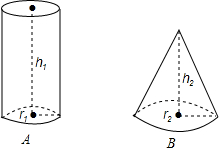 如图所示,已知B的底面周长比A大2πcm,r1:r2=2:3,VA比VB多$\frac{2}{3}$,h1+h2=18cm.问:
如图所示,已知B的底面周长比A大2πcm,r1:r2=2:3,VA比VB多$\frac{2}{3}$,h1+h2=18cm.问:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y2<y1<y3 | D. | y2<y3<y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在数学活动中,小明为了求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值(结果用n表示),设计如图所示的几何图形,请你利用这个几何图形求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为1-$\frac{1}{{2}^{n}}$.
在数学活动中,小明为了求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值(结果用n表示),设计如图所示的几何图形,请你利用这个几何图形求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为1-$\frac{1}{{2}^{n}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com