
 在边长为1的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C(不与A、B重合,且A、B、C三点不在同一条直线上),
在边长为1的小正方形组成的网格中,有如图所示的A,B两点,在格点上任意放置点C(不与A、B重合,且A、B、C三点不在同一条直线上),分析 (1)由任意放置点C(不与A、B重合,且A、B、C三点不在同一条直线上),共有13种等可能的结果,其中恰好能使得△ABC的面积为1的有4种情况,直接利用概率公式求解即可求得答案;
(2)由能使△ABC为等腰三角形的有5个,直接利用概率公式求解即可求得答案.
解答 解:(1)∵任意放置点C(不与A、B重合,且A、B、C三点不在同一条直线上),共有13种等可能的结果,
如图1,其中恰好能使得△ABC的面积为1的有4种情况,
∴恰好能使得△ABC的面积为1的概率为:$\frac{4}{13}$;
(2)∵如图2,能使△ABC为等腰三角形的有6个,
∴能使△ABC为等腰三角形的概率为:$\frac{6}{13}$.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:选择题
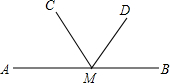 如图,已知点M是直线AB上一点,∠AMC=52°48′,∠BMD=72°19°,则∠CMD等于( )
如图,已知点M是直线AB上一点,∠AMC=52°48′,∠BMD=72°19°,则∠CMD等于( )| A. | 49°07′ | B. | 54°53′ | C. | 55°53′ | D. | 53°7′ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y+1>x-1 | B. | $\frac{x}{3}$>$\frac{y}{3}$ | C. | 1-x>1-y | D. | -3x>-3y |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-7)+(-7)=0 | B. | (-$\frac{1}{10}$)-(+$\frac{1}{10}$)=0 | C. | 0+(-101)=101 | D. | (+$\frac{1}{3}$)+(-$\frac{1}{2}$)=-$\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com