
”¾ĢāÄæ”æŌŚ2018“ŗ¼¾»·¾³ÕūÖĪ»ī¶ÆÖŠ£¬Ä³ÉēĒų¼Ę»®¶ŌĆ껿ĪŖ1600m2µÄĒųÓņ½ųŠŠĀĢ»Æ£®¾Ķ¶±ź£¬Óɼה¢ŅŅĮ½øö¹¤³Ģ¶ÓĄ“Ķź³É£¬Čō¼×¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆµÄĆ껿ŹĒŅŅ¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆĆ껿µÄ2±¶£¬²¢ĒŅŌŚ¶ĄĮ¢Ķź³ÉĆ껿ĪŖ400m2ĒųÓņµÄĀĢ»ÆŹ±£¬¼×¶Ó±ČŅŅ¶ÓÉŁÓĆ5Ģģ£®
(1)Ēó¼×”¢ŅŅĮ½¹¤³Ģ¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆµÄĆ껿£»
(2)Éč¼×¹¤³Ģ¶ÓŹ©¹¤xĢģ£¬ŅŅ¹¤³Ģ¶ÓŹ©¹¤yĢģ£¬øÕŗĆĶź³ÉĀĢ»ÆČĪĪń£¬Ēóy¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½£»
(3)Čō¼×¶ÓĆæĢģĀĢ»Æ·ŃÓĆŹĒ0.6ĶņŌŖ£¬ŅŅ¶ÓĆæĢģĀĢ»Æ·ŃÓĆĪŖ0.25ĶņŌŖ£¬ĒŅ¼×ŅŅĮ½¶ÓŹ©¹¤µÄ×ÜĢģŹż²»³¬¹ż25Ģģ£¬ŌņČēŗĪ°²Åż×ŅŅĮ½¶ÓŹ©¹¤µÄĢģŹż£¬Ź¹Ź©¹¤×Ü·ŃÓĆ×īµĶ£æ²¢Ēó³ö×īµĶ·ŃÓĆ£®
”¾“š°ø”æ£Ø1£©¼×”¢ŅŅĮ½¹¤³Ģ¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆµÄĆ껿·Ö±šĪŖ80m2”¢40m2£»£Ø2£©y£½©2x+40£»£Ø3£©µ±x£½15Ź±£¬W×īµĶ£½11.5
”¾½āĪö”æ
£Ø1£©Éč³öĮ½¶ÓµÄĆæĢģĀĢ»ÆµÄĆ껿£¬ŅŌĮ½¶Ó¹¤×÷Ź±¼äĪŖµČĮæ¹¹Ōģ·ÖŹ½·½³Ģ£»
£Ø2£©ŅŌ£Ø1£©ĪŖ»ł“”±ķŹ¾¼×ŅŅĮ½¶Ó·Ö±š¹¤×÷xĢģ”¢yĢģµÄ¹¤×÷×ÜĮ棬¹¤×÷×ÜĮæŗĶĪŖ1600£»
£Ø3£©ÓĆ¼×ŅŅĮ½¶ÓŹ©¹¤µÄ×ÜĢģŹż²»³¬¹ż25ĢģČ·¶Ø×Ō±äĮæxȔֵ·¶Ī§£¬ÓĆx±ķŹ¾×ÜŹ©¹¤·ŃÓĆ£¬øł¾ŻŅ»“ĪŗÆŹżŌö¼õŠŌĒóµĆ×īµĶ·ŃÓĆ£®
½ā£ŗ£Ø1£©ÉčŅŅ¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆĆ껿ĪŖam2£¬Ōņ¼×¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆĆ껿ĪŖ2am2
øł¾ŻĢāŅāµĆ£ŗ ![]()
½āµĆa£½40
¾¼ģŃ飬a£½40ĪŖŌ·½³ĢµÄ½ā
Ōņ¼×¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆĆ껿ĪŖ80m2
“š£ŗ¼×”¢ŅŅĮ½¹¤³Ģ¶ÓĆæĢģÄÜĶź³ÉĀĢ»ÆµÄĆ껿·Ö±šĪŖ80m2”¢40m2
£Ø2£©ÓÉ£Ø1£©µĆ80x+40y£½1600
ÕūĄķµĆ£ŗ y£½©2x+40
£Ø3£©ÓÉŅŃÖŖy+x”Ü25
”ą©2x+40+x”Ü25
½āµĆx”Ż15
×Ü·ŃÓĆW£½0.6x+0.25y£½0.6x+0.25£Ø©2x+40£©£½0.1x+10
”ßk£½0.1£¾0
”ąWĖęxµÄŌö“ó¶ųŌö“ó
”ąµ±x£½15Ź±£¬W×īµĶ£½1.5+10£½11.5


 ¾ŁŅ»·“Čżµ„ŌŖĶ¬²½¹ż¹Ų¾ķĻµĮŠ“š°ø
¾ŁŅ»·“Čżµ„ŌŖĶ¬²½¹ż¹Ų¾ķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔Ć÷ÓŠ 5 ÕÅŠ“×Ų»Ķ¬Źż×ÖµÄæØʬ£¬ĒėÄć°“ŅŖĒó³é³öæØʬ£¬Ķź³ÉĻĀĮŠø÷ĪŹĢā£ŗ
![]()
£Ø1£©“ÓÖŠČ”³ö 2 ÕÅæØʬ£¬Ź¹Õā 2 ÕÅæØʬÉĻŹż×ֵijĖ»ż×ī“󣬳Ė»żµÄ×ī“óÖµĪŖ £»
£Ø2£©“ÓÖŠČ”³ö 2 ÕÅæØʬ£¬Ź¹Õā 2 ÕÅæØʬÉĻŹż×ÖĻą³żµÄÉĢ×īŠ”£¬ÉĢµÄ×īŠ”ÖµĪŖ £»
£Ø3£©“ÓÖŠČ”³ö 4 ÕÅæØʬ£¬ÓĆѧ¹żµÄŌĖĖć·½·Ø£¬Ź¹½į¹ūĪŖ 24£®Š“³öŌĖĖćŹ½×Ó£®£ØŠ“³öŅ»ÖÖ¼“æÉ£©Ėć 24 µÄŹ½×ÓĪŖ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔“ĻÓėŠ”Ć÷ŌŚŅ»ÕžŲŠĪĢØĒņץABCD±ß“ņĢØĒņ£¬øĆĒņץ³¤AB=4m£¬æķAD=2m£¬µćO”¢E·Ö±šĪŖAB”¢CDµÄÖŠµć£¬ŅŌAB”¢OEĖłŌŚµÄÖ±Ļß½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµ”£

£Ø1£©ČēĶ¼1£¬MĪŖBCÉĻŅ»µć£»
¢ŁŠ”Ć÷ŅŖ½«Ņ»Ēņ“ÓµćM»÷³öÉäĻņ±ßAB£¬¾·“µÆĀäČėD“ü£¬ĒėÄć»³öABÉĻµÄ·“µÆµćFµÄĪ»ÖĆ£»
¢ŚČō½«Ņ»Ēņ“ÓµćM(2£¬12)»÷³öÉäĻņ±ßABÉĻµćF(0.5£¬0)£¬ĪŹøĆĒņ·“µÆŗóÄÜ·ńײµ½Ī»ÓŚ(-0.5£¬0.8)Ī»ÖƵÄĮķŅ»Ēņ?ĒėĖµĆ÷ĄķÓÉ
£Ø2£©ČēĶ¼2£¬ŌŚĒņץÉĻ·ÅÖĆĮ½øöµ²°å(ŗń¶Č²»¼Ę)µ²°åMQµÄ¶ĖµćMŌŚADÖŠµćÉĻĒŅMQ”ĶAD£¬MQ=2m£¬µ²°åEHµÄ¶ĖµćHŌŚ±ßBCÉĻ»¬¶Æ£¬ĒŅµ²°åEH¾¹żDCµÄÖŠµćE£»
¢ŁŠ”“Ļ°ŃĒņ“ÓBµć»÷³ö£¬ŗó¾µ²°åEH·“µÆŗóĀäČėD“ü£¬µ±HŹĒBCÖŠµćŹ±£¬ŹŌÖ¤Ć÷£ŗDN=BN£»
¢ŚČēĶ¼3£¬Š”Ć÷°ŃĒņ“ÓBµć»÷³ö£¬ŅĄ“Ī¾µ²°åEHŗĶµ²°åMQ·“µÆŅ»“ĪŗóĀäČėD“ü£¬ŅŃÖŖ”ĻEHC=75”ć£¬ĒėÄćÖ±½ÓŠ“³öĒņµÄŌĖ¶ÆĀ·¾¶BN+NP+PDµÄ³¤”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÕŅ¹ęĀɲ¢½ā“šĪŹĢā.
(1)°“ĻĀĶ¼·½Ź½°Ś·ÅŗŚÉ«Ī§Ęå×Ó£¬ĢīŅ»Ģī£¬ĆæøöĶ¼¹²Šč¼øƶĘå×Ó.

Ķ¼µÄĖ³Šņ |
|
|
|
|
|
ŠčŅŖµÄĘå×ÓŹż/ƶ |
|
(2)øł¾ŻÄć·¢ĻֵĹęĀÉ£¬ĖćŅ»Ė浌![]() øöĶ¼£¬¹²ŠčŅŖ( )ƶĘå×Ó.
øöĶ¼£¬¹²ŠčŅŖ( )ƶĘå×Ó.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬![]() ŹĒÖ±Ļß
ŹĒÖ±Ļß![]() ÉĻŅ»µć£¬
ÉĻŅ»µć£¬![]() ĪŖČĪŅ»ĢõÉäĻߣ¬
ĪŖČĪŅ»ĢõÉäĻߣ¬![]() Ę½·Ö
Ę½·Ö![]() £¬
£¬![]() Ę½·Ö
Ę½·Ö![]() .
.

£Ø1£©ÕŅ³öĶ¼ÖŠ![]() µÄ²¹½Ē£¬
µÄ²¹½Ē£¬![]() µÄ²¹½Ē£»
µÄ²¹½Ē£»
£Ø2£©Čō![]() £¬Ēó
£¬Ēó![]() ŗĶ
ŗĶ![]() µÄ¶ČŹż£»
µÄ¶ČŹż£»
£Ø3£©![]() Óė
Óė![]() ¾ßÓŠŌõŃłµÄŹżĮæ¹ŲĻµ£æĖµĆ÷ĄķÓÉ.
¾ßÓŠŌõŃłµÄŹżĮæ¹ŲĻµ£æĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŹī¼ŁĘŚ¼ä£¬Š”Ć÷ŗĶŠ”Ó±Į½¼Ņ¹²8ČĖĻąŌ¼Ķā³öĀĆŠŠ£¬·Ö±š³Ė×ųĮ½Į¾³ö×ā³µĒ°Ķł»ś³”ŌŚ¾ąĄė»ś³”11Ē§Ćד¦Ņ»Į¾³µ³öĮĖ¹ŹÕĻ²»ÄܼĢŠųŠŠŹ».“ĖŹ±Ąė»ś³”Ķ£Ö¹°ģĄķµĒ»śŹÖŠų»¹ÓŠ30·ÖÖÓ£¬ĪØŅ»æÉŅŌĄūÓĆµÄ½»Ķع¤¾ßÖ»ÓŠĮķŅ»Į¾³ö×ā³µ£¬Į¬Ķ¬Ė¾»śŌŚÄŚĻŽ³Ė5ČĖ£¬³µĖŁĆ抔Ź±60Ē§Ć×.
(1)Čē¹ūÕāĮ¾³µ·ÖĮ½Åś½ÓĖĶ£¬ĘäÖŠ4ČĖ³Ė³µĻČ×ߣ¬ÓąĻĀ4ČĖŌµŲµČŗņ£¬8ČĖÄÜ·ń¼°Ź±µ½“ļ»ś³”°ģĄķµĒ»śŹÖŠų£æ(ÉĻĻĀ³µŹ±¼äŗöĀŌ²»¼Ę)
(2)Čē¹ūÕāĮ¾³µŌŚĖĶµŚŅ»ÅśæĶČĖµÄŹ±ŗņ£¬ÓąĻĀµÄČĖŅŌĆ抔Ź±6Ē§Ć×µÄĖŁ¶Č²½ŠŠĒ°Ķł»ś³”£¬“żĖ¾»ś½«µŚŅ»ÅśæĶČĖĖĶ“ļŗóĮ¢¼“·µ»Ų½ÓµŚ¶žÅśæĶČĖ£¬ĖūĆĒÄܼ°Ź±µ½“ļ»ś³”Āš£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
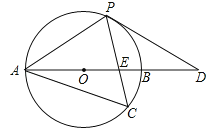
”¾ĢāÄæ”æČēĶ¼£¬ŅŌAB±ßĪŖÖ±¾¶µÄ”ŃO¾¹żµćP£¬CŹĒ”ŃOÉĻŅ»µć£¬Į¬½įPC½»ABÓŚµćE£¬ĒŅ”ĻACP=60”ć£¬PA=PD£®
£Ø1£©ŹŌÅŠ¶ĻPDÓė”ŃOµÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©ČōµćCŹĒ»”ABµÄÖŠµć£¬ŅŃÖŖAB=4£¬ĒóCECPµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ(12·Ö)(2017”¤»ĘøŌ)ŅŃÖŖ£ŗČēĶ¼£¬Ņ»“ĪŗÆŹży£½£2x£«1Óė·“±ČĄżŗÆŹży£½![]() µÄĶ¼ĻóÓŠĮ½øö½»µćA(£1£¬m)ŗĶB£¬¹żµćA×÷AE”ĶxÖį£¬“¹×ćĪŖE£»¹żµćB×÷BD”ĶyÖį£¬“¹×ćĪŖµćD£¬ĒŅµćDµÄ×ų±źĪŖ(0£¬£2)£¬Į¬½įDE.
µÄĶ¼ĻóÓŠĮ½øö½»µćA(£1£¬m)ŗĶB£¬¹żµćA×÷AE”ĶxÖį£¬“¹×ćĪŖE£»¹żµćB×÷BD”ĶyÖį£¬“¹×ćĪŖµćD£¬ĒŅµćDµÄ×ų±źĪŖ(0£¬£2)£¬Į¬½įDE.
(1)ĒókµÄÖµ£»
(2)ĒóĖıߊĪAEDBµÄĆ껿£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ°ŃĆüĢā”°Čē¹ūÖ±½ĒČż½ĒŠĪµÄĮ½Ö±½Ē±ß³¤·Ö±šĪŖa”¢b£¬Š±±ß³¤ĪŖc£¬ÄĒĆ“![]() ”±µÄÄęĆüĢāøÄŠ“³É”°Čē¹ū””£¬ÄĒĆ“”””±µÄŠĪŹ½£ŗ_____________________________
”±µÄÄęĆüĢāøÄŠ“³É”°Čē¹ū””£¬ÄĒĆ“”””±µÄŠĪŹ½£ŗ_____________________________
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com