练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知平行四边形，过做于点，，若在平行四边形内取一点，则该点到平行四边形的四个顶点的距离均不小于1的概率为_______．

    【答案】

    【解析】

    根据题意以平行四边形ABCD的各个顶点为圆心、半径为1作圆如图所示，可得当该点位于图中阴影部分区域时，它到四个顶点的距离均不小于1.因此算出平行四边形ABCD的面积和阴影部分区域的面积，利用几何概率计算公式加以计算，即可得到所求的概率.

    解：分别以平行四边形ABCD的各个顶点为圆心，作半径为1的圆，如图所示：

    在平行四边形ABCD内任取一点P，则点P位于四个圆的外部或在圆上时，满足点P到四个顶点的距离均不小于1，即图中的阴影部分区域

    ∵，

    ∴S阴影=S平行四边形ABCD-S空白=32-π×12=32-π.

    因此，该点到四个顶点的距离均不小于1的概率：.

    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】四川雅安发生地震后，某校学生会向全校1900名学生发起了“心系雅安”捐款活动，为了解捐款情况，学会生随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列是问题：

    （1）本次接受随机抽样调查的学生人数为　　　　，图①中m的值是　　　　；

    （2）求本次调查获取的样本数据的平均数、众数和中位数；

    （3）根据样本数据，估计该校本次活动捐款金额为10元的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】王老师为学校购买运动会的奖品后，回学校向后勤处赵主任交账说：我买了两种书共105本，单价分别为8元和12元，买书前我领了1600元，现在还余518元．赵主任算了一下说：你肯定搞错了．

    （1）赵主任为什么说他搞错了，请你用方程组的知识给予解释；

    （2）王老师连忙拿出购物发票，发现的确弄错了，因为他还买了一个笔记本，但笔记本的单价已模糊不清，只能辨认出应为小于5元的整数，笔记本的单价可能为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为创建“书香校园”，购置了一批图书，已知购买科普类图书花费10000元，购买文学类图书花费9000元，其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元，且购买科普类图书的数量与购买文学类图书的数量相等．求科普类图书平均每本的价格．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在中，若存在一个内角角度，是另外一个内角角度的倍（为大于1的正整数），则称为倍角三角形．例如，在中，，，，可知，所以为3倍角三角形．

    （1）在中，，，则为________倍角三角形；

    （2）若是3倍角三角形，且其中一个内角的度数是另外一个内角的余角的度数的，求的最小内角．

    （3）若是2倍角三角形，且，请直接写出的最小内角的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某风景区内的公路如图1所示，景区内有免费的班车，从入口处出发，沿该公路开往草甸，途中停靠塔林（上下车时间忽略不计），第一班车上午8点发车，以后每隔10分钟有一班车从入口处发车，小聪周末到该风景区游玩，上午7：40到达入口处，因还没到班车发车时间，于是从景区入口处出发，沿该公路步行25分钟后到达塔林，离入口处的路程（米）与时间（分）的函数关系如图2所示．

    （1）求第一班车从入口处到达塔林的时间．

    （2）小聪在塔林游玩40分钟后，想坐班车到草甸，则小聪最早能够坐上第几班车？如果他坐这班车到草甸，比他在塔林游玩结束后立即步行到草甸提早了几分钟？（假设每一班车速度均相同，小聪步行速度不变）．

    （3）若小聪在8：30至8：50之间到达发车站乘坐班车，且到达发车站的时刻是随机的，则他等车时间不超过3分钟的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，A(﹣1，5)，B(﹣1，0)，C(﹣4，3).

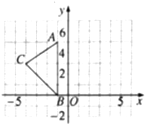
    ⑴请画出△ABC关于y轴对称的△A’B’C’(其中A’，B’，C’分別是A，B，C的对应点，不写画法)；

    ⑵直接写出A’，B’，C’三点的坐标：A’ ( )，B’( )，C’( )；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，顶点为A的抛物线y=a（x+2）2﹣4交x轴于点B（1，0），连接AB，过原点O作射线OM∥AB，过点A作AD∥x轴交OM于点D，点C为抛物线与x轴的另一个交点，连接CD．

    （1）求抛物线的解析式；
    （2）若动点P从点O出发，以每秒1个单位长度的速度沿着射线OM运动，设点P运动的时间为t秒，问：当t为何值时，OB=AP；
    （3）若动点P从点O出发，以每秒1个单位长度的速度沿线段OD向点D运动，同时动点Q从点C出发，以每秒2个单位长度的速度沿线段CO向点O运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动时间为t秒，连接PQ．问：当t为何值时，四边形CDPQ的面积最小？并求此时PQ的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD，如图1，再在矩形纸板的四个角上切去边长相等的小正方形，再把它的边沿虚线折起，做成一个无盖的长方体纸盒，底面为矩形EFGH，如图2．设小正方形的边长为x厘米．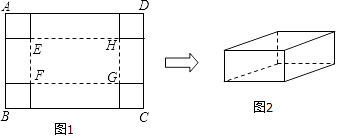

    （1）当矩形纸板ABCD的一边长为90厘米时，求纸盒的侧面积的最大值；
    （2）当EH：EF=7：2，且侧面积与底面积之比为9：7时，求x的值．

    查看答案和解析>>

    同步练习册答案