
【题目】某种蔬菜的单价![]() 与销售月份x之间的关系如图1所示,成本
与销售月份x之间的关系如图1所示,成本![]() 与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
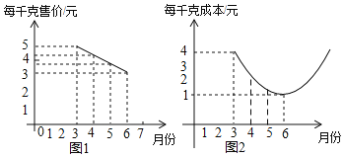
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的利润是 元.(利润=售价-成本);
(2)设每千克该蔬菜销售利润为P,请列出x与P之间的函数关系式,并求出哪个月出售这种蔬菜每千克的利润最大,最大利润是多少?
【答案】(1)2;(2)5月时利润最大,最大利润为![]() 元.
元.
【解析】
(1)找出当x=6时,y1、y2的值,二者做差即可得出结论;
(2)观察图象找出点的坐标,利用待定系数法即可求出y1、y2关于x的函数关系式,二者做差后利用二次函数的性质即可解决最值问题.
(1)当x=6时,y1=3,y2=1.
∵y1﹣y2=3﹣1=2,∴6月份出售这种蔬菜每千克的收益是2元.
(2)设y1=mx+n,y2=a(x﹣6)2+1.
将(3,5)、(6,3)代入y1=mx+n,得![]() ,解得:
,解得: ,∴y1
,∴y1![]() x+7;
x+7;
将(3,4)代入y2=a(x﹣6)2+1,4=a(3﹣6)2+1,解得:a![]() ,∴y2
,∴y2![]() (x﹣6)2+1
(x﹣6)2+1![]() x2﹣4x+13,∴P=y1﹣y2
x2﹣4x+13,∴P=y1﹣y2![]() x+7﹣(
x+7﹣(![]() x2﹣4x+13)
x2﹣4x+13)![]() x2
x2![]() x﹣6
x﹣6![]() (x﹣5)2
(x﹣5)2![]() .
.
∵![]() 0,∴当x=5时,P取最大值,最大值为
0,∴当x=5时,P取最大值,最大值为![]() .
.
答:5月份出售这种蔬菜,每千克的收益最大,最大利润是![]() 元/千克.
元/千克.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】)如图,Rt△ABC中,C= 90o,以斜边AB为边向外作正方形 ABDE,且正方形对角线交于点D,连接OC,已知AC=5,OC=6![]() ,则另一直角边BC的长为 ▲ .
,则另一直角边BC的长为 ▲ .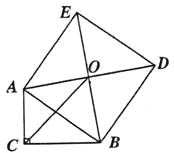
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(a,1)、B(﹣1,b)都在函数![]() (x<0)的图象上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是 .
(x<0)的图象上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A在x轴负半轴上,顶点B在x轴正半轴上.若抛物线p=ax2-10ax+8(a>0)经过点C、D,则点B的坐标为________.
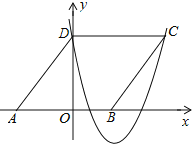
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个面积为150平方米的长方形养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙,墙长为18米,另三边用篱笆围成,如篱笆长度为35米,且要求用完。求鸡场的长与宽各是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
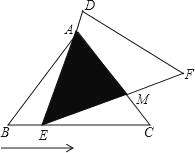
【题目】如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;
(3)当线段AM最短时,求重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
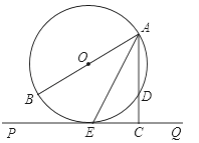
【题目】如图,AB为⊙O的直径,PQ切⊙O于E,AC⊥PQ于C,交⊙O于D.
(1)求证:AE平分∠BAC;
(2)若AD=2,EC=![]() ,∠BAC=60°,求⊙O的半径.
,∠BAC=60°,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数![]() 上一个动点,
上一个动点,![]() 轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会
轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会![]()
![]()

A. 先增后减 B. 先减后增 C. 逐渐减小 D. 逐渐增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com