

分析 (1)甲列方程时的等量关系为:朱老师来回时所走的路程相等;
乙列方程时的等量关系为:两次走同样的路程时行驶的速度差为10;
(2)根据(1)所列的方程进行解答即可.
解答 解:(1)甲:设朱老师驾车从江都到上海的平均速度是x千米/小时,则从江都到上海的路程是不变量,即4.5x=(4.5-0.5)(x+10).
乙:设朱老师从江都到上海的路程为y,则根据他们的来、回时的速度差为10千米得到:$\frac{y}{4.5-0.5}$-$\frac{y}{4.5}$=10.
故答案是:去时的平均速度;从江都到上海的路程;
方框内该填:x+10; 4; 4.5;
(2)甲的方法:
设去时的平均速度为x千米/时,则返回时的平均速度为(x+10)千米/时,则
4.5x=(4.5-0.5)(x+10)
解得x=804.
5x=4.5×80=360.
答:江都与上海两地间的高速公路路程是360千米.
或乙的方法:
设江都与上海两地间的高速公路路程是y千米.$\frac{y}{4.5-0.5}-\frac{y}{4.5}=10$,
解得y=360.
答:江都与上海两地间的高速公路路程是360千米.
点评 本题考查了一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.


科目:初中数学 来源: 题型:解答题
 解不等式组,并把解集在数轴上表示出来.
解不等式组,并把解集在数轴上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
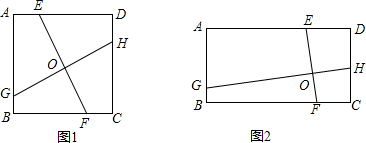
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,AB=6cm,AD=AC=5cm,点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF,若运动时间为t(s)(0<t<2.5).解答下列问题:
如图,在?ABCD中,AB=6cm,AD=AC=5cm,点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF,若运动时间为t(s)(0<t<2.5).解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com