
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌИјГіШчЯТЖЈвхЃКаЮШчy=ЃЈxЉmЃЉЃЈxЉm+1ЃЉгыy=ЃЈxЉmЃЉЃЈxЉmЉ1ЃЉЕФСНИіЖўДЮКЏЪ§ЕФЭМЯѓНазіажЕмХзЮяЯпЃЎ
ЃЈ1ЃЉЪдаДГівЛЖдажЕмХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉШєЖўДЮКЏЪ§y=x2ЉxЃЈЭМЯѓШчЭМЃЉгыy=x2Љbx+2ЕФЭМЯѓЪЧажЕмХзЮяЯпЃЎ
ЂйЧѓbЕФжЕЃЎ
ЂкШєжБЯпy=kгыетЖдажЕмХзЮяЯпгаЫФИіНЛЕуЃЌДгзѓЭљгввРДЮЮЊAЃЌBЃЌCЃЌDЫФИіЕуЃЌШєЕуBЃЌЕуCЮЊЯпЖЮADШ§ЕШЗжЕуЃЌЧѓЯпЖЮBCЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉНЋm=0ДњШыy=ЃЈxЉmЃЉЃЈxЉm+1ЃЉгыy=ЃЈxЉmЃЉЃЈxЉmЉ1ЃЉЃЌМДПЩЕУЕНвЛЖдажЕмХзЮяЯп
ЃЈ2ЃЉЂйy=x2Љx=xЃЈxЉ1ЃЉЃЎЗжСНжжЧщПіЬжТлЃК
ЧщПівЛЃКШєy=xЃЈxЉ1ЃЉЪЧаЮШчy=ЃЈxЉmЃЉЃЈxЉm+1ЃЉЃЌЧѓГіm=1ЃЌЕУЕНСэвЛИіКЏЪ§НтЮіЪНЃЌНјЖјЕУГіbЕФжЕЃЛ
ЧщПіЖўЃКШєy=xЃЈxЉ1ЃЉЪЧаЮШчy=ЃЈxЉmЃЉЃЈxЉmЉ1ЃЉЃЌЭЌРэЧѓНтЃЛ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉНЋm=0ДњШыy=ЃЈxЉmЃЉЃЈxЉm+1ЃЉгыy=ЃЈxЉmЃЉЃЈxЉmЉ1ЃЉЃЌМДПЩЕУЕНвЛЖдажЕмХзЮяЯпЃЛ
ЃЈ2ЃЉЂйy=x2Љx=xЃЈxЉ1ЃЉЃЎЗжСНжжЧщПіЬжТлЃК
ЧщПівЛЃКШєy=xЃЈxЉ1ЃЉЪЧаЮШчy=ЃЈxЉmЃЉЃЈxЉm+1ЃЉЃЌЧѓГіm=1ЃЌЕУЕНСэвЛИіКЏЪ§НтЮіЪНЃЌНјЖјЕУГіbЕФжЕЃЛ
ЧщПіЖўЃКШєy=xЃЈxЉ1ЃЉЪЧаЮШчy=ЃЈxЉmЃЉЃЈxЉmЉ1ЃЉЃЌЭЌРэЧѓНтЃЛ
ЂкИљОнЦНвЦЕФЙцТЩПЩжЊЃЌy=x2Љ3x+2ЕФЭМЯѓПЩвдПДзїЪЧгЩy=x2ЉxЕФЭМЯѓЯђгвЦНвЦ1ИіЕЅЮЛЕУЕНЃЌЗжСНжжЧщПіЃКШчЙћkЃО0ЃЌдђЕуAгыЕуBЪЧЦНвЦЖдгІЕуЃЌAB=1ЃЌдйИљОнШ§ЕШЗжЕуЕФЖЈвхМДПЩЧѓНтЃЛШчЙћkЃМ0ЃЌдђЕуAгыЕуCЪЧЦНвЦЖдгІЕуЃЌAC=1ЃЌЭЌРэЧѓНтМДПЩЃЎ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉЕБm=0ЪБЃЌЕУЕНвЛЖдажЕмХзЮяЯпЃЌ
y=xЃЈx+1ЃЉгыy=xЃЈxЉ1ЃЉЃЛ
ЃЈ2ЃЉЂйy=x2Љx=xЃЈxЉ1ЃЉЃЎ
ЧщПівЛЃКШєy=xЃЈxЉ1ЃЉЪЧаЮШчy=ЃЈxЉmЃЉЃЈxЉm+1ЃЉЃЌдђm=1ЃЌдђСэвЛИіКЏЪ§ЮЊy=ЃЈxЉ1ЃЉЃЈxЉ2ЃЉЃЌМДy=x2Љ3x+2ЃЌb=3ЃЎ
ЧщПіЖўЃКШєy=xЃЈxЉ1ЃЉЪЧаЮШчy=ЃЈxЉmЃЉЃЈxЉmЉ1ЃЉЃЌдђm=0ЃЌдђСэвЛИіКЏЪ§ЮЊy=xЃЈxЉ1ЃЉЃЌМДy=x2ЉxЃЌгывбжЊУЌЖмЃЎ
Ђкy=x2Љ3x+2ЕФЭМЯѓПЩвдПДзїЪЧгЩy=x2ЉxЕФЭМЯѓЯђгвЦНвЦ1ИіЕЅЮЛЕУЕНЃЌШчЭМЃЎ
ШчЙћkЃО0ЃЌдђЕуAгыЕуBЪЧЦНвЦЖдгІЕуЃЌAB=1ЃЌ
ЁпЕуBЃЌЕуCЮЊЯпЖЮADШ§ЕШЗжЕуЃЌ
ЁрAB=BC=CD=![]() AD=1ЃЌМДBC=1ЃЛ
AD=1ЃЌМДBC=1ЃЛ
ШчЙћkЃМ0ЃЌдђЕуAгыЕуCЪЧЦНвЦЖдгІЕуЃЌAC=1ЃЌ
ЁпЕуBЃЌЕуCЮЊЯпЖЮADШ§ЕШЗжЕуЃЌ
ЁрAB=BC=![]() AC=
AC=![]() ЃЌМДBC=
ЃЌМДBC=![]() ЃЎ
ЃЎ
ЙЪЯпЖЮBCЕФГЄЮЊ1Лђ![]() ЃЎ
ЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтжаЮЊМйУќЬтЕФЪЧЃЈ ЃЉ
A. ФкДэНЧЯрЕШЃЌСНжБЯпЦНаа
B. ЭЌвЛЦНУцФкСНЬѕжБЯпБЛЕкШ§ЬѕжБЯпЫљНиЃЌЭЌХдФкНЧЛЅВЙ
C. вЛИіЖлНЧЕФВЙНЧБиЪЧШёНЧ
D. Й§СНЕугаЧвжЛгавЛЬѕжБЯп
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌЙЋТЗЩЯгаAЁЂBЁЂCШ§ИіГЕеОЃЌвЛСОЦћГЕДгAеОвдЫйЖШv1дШЫйЪЛЯђBеОЃЌЕНДяBеОКѓВЛЭЃСєЃЌвдЫйЖШv2дШЫйЪЛЯђCеОЃЌЦћГЕааЪЛТЗГЬyЃЈЧЇУзЃЉгыааЪЛЪБМфxЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЭМЯѓШчЭМЃЈ2ЃЉЫљЪОЃЎ
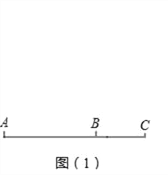
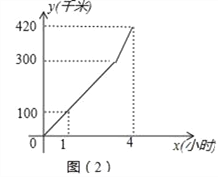
ЃЈ1ЃЉЕБЦћГЕдкAЁЂBСНеОжЎМфдШЫйааЪЛЪБЃЌЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНМАздБфСПЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЧѓГіv2ЕФжЕЃЛ
ЃЈ3ЃЉШєЦћГЕдкФГвЛЖЮТЗГЬФкИеКУгУ50ЗжжгааЪЛСЫ90ЧЇУзЃЌЧѓетЖЮТЗГЬПЊЪМЪБxЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭМЂйЪЧвЛУцОиаЮВЪЦьЭъШЋеЙЦНЪБЕФГпДчЭМЃЈЕЅЮЛЃКcmЃЉЃЎЦфжаОиаЮABCDЪЧгЩЫЋВуАзВМЗьжЦЕФДЉЦьИЫгУЕФЦьПуЃЌвѕгАВПЗжDCEFЮЊОиаЮГёЖаЦьУцЃЎ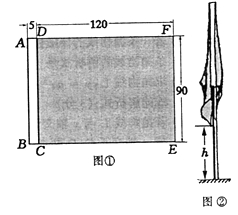
ЃЈ1ЃЉгУОМгЙЄЕФдВФОИЫДЉШыЦьПузїЦьИЫЃЌЧѓЦьИЫЕФзюДѓжБОЖЃЈОЋШЗЕН1cmЃЉЃЛ
ЃЈ2ЃЉНЋДЉКУВЪЦьЕФЦьИЫДЙжБВхдкВйГЁЩЯЃЌЦьИЫДгЦьЖЅЕНЕиУцЕФИпЖШЮЊ220cmЃЎдкЮоЗчЕФЬьЦјРяЃЌВЪЦьздШЛЯТДЙЃЌШчЭМЂкЃЎЧѓВЪЦьЯТДЙЪБзюЕЭДІРыЕиУцЕФзюаЁИпЖШhЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГОЯњЕъОЯњвЛжжНЈжўВФСЯЃЌЕБУПЖжЪлМлЮЊ260дЊЪБЃЌдТЯњЪлСПЮЊ45ЖжЃЎИУОЯњЕъЮЊЬсИпОгЊРћШѓЃЌзМБИВЩШЁНЕМлЕФЗНЪННјааДйЯњЃЎОЪаГЁЕїВщЗЂЯжЃКЕБУПЖжЪлМлУПЯТНЕ10дЊЪБЃЌдТЯњЪлСПОЭЛсдіМг7.5ЖжЃЎзлКЯПМТЧИїжжвђЫиЃЌУПЪлГівЛЖжНЈжўВФСЯЙВашГЩБОМАЦфЫќЗбгУ100дЊЃЎЩшУПЖжВФСЯЪлМлЮЊxЃЈдЊЃЉЃЌИУОЯњЕъЕФдТРћШѓЮЊyЃЈдЊЃЉЃЎ
ЃЈ1ЃЉЧѓГіyгыxЕФКЏЪ§ЙиЯЕЪНЃЈВЛвЊЧѓаДГіxЕФШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ2ЃЉИУОЯњЕъвЊЛёЕУзюДѓдТРћШѓЃЌЪлМлгІЖЈЮЊУПЖжЖрЩйдЊЃЛ
ЃЈ3ЃЉаЁЭѕЫЕЃКЁАЕБдТРћШѓзюДѓЪБЃЌдТЯњЪлЖювВзюДѓЃЎЁБФуШЯЮЊЖдТ№ЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=ax2+bx+cЙ§ЕуAЃЈ1ЃЌ0ЃЉЃЌBЃЈЉ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ3ЃЉ
ЃЈ1ЃЉЧѓДЫЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкХзЮяЯпЩЯДцдквЛЕуPЪЙЁїABPЕФУцЛ§ЮЊ6ЃЌЧѓЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAEЪЧЮЛгкЙЋТЗБпЕФЕчЯпИЫЃЌЮЊСЫЪЙРЯпCDEВЛгАЯьЦћГЕЕФе§ГЃааЪЛЃЌЕчСІВПУХдкЙЋТЗЕФСэвЛБпЪњСЂСЫвЛИљЫЎФрГХИЫBDЃЌгУгкГХЦ№РЯпЃЎвбжЊЙЋТЗЕФПэABЮЊ8УзЃЌЕчЯпИЫAEЕФИпЮЊ12УзЃЌЫЎФрГХИЫBDИпЮЊ6УзЃЌРЯпCDгыЫЎЦНЯпACЕФМаНЧЮЊ67.4ЁуЃЎЧѓРЯпCDEЕФзмГЄLЃЈAЁЂBЁЂCШ§ЕудкЭЌвЛжБЯпЩЯЃЌЕчЯпИЫЁЂЫЎФрИЫЕФДѓаЁКіТдВЛМЦЃЉЃЎЃЈВЮПМЪ§ОнЃКsin67.4ЁуЁж![]() ЃЌcos67.4ЁуЁж
ЃЌcos67.4ЁуЁж![]() ЃЌtan67.4ЁуЁж
ЃЌtan67.4ЁуЁж![]() ЃЉ
ЃЉ
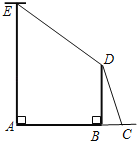
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊa+b=3ЃЌab=2ЃЌдђa2+b2ЕФжЕЮЊЃЈ ЃЉ
A. 3 B. 4 C. 5 D. 6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDжаЃЌЁЯBЃН60ЁуЃЌABЃН4ЃЌдђвдACЮЊБпЕФе§ЗНаЮACEFЕФжмГЄЮЊ(ЁЁЁЁ)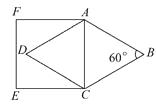
A.14
B.15
C.16
D.17
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com