
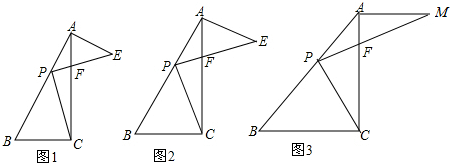
分析 (1)①根据相似三角形判定的方法,判断出∠EAF=∠PBC、∠EFA=∠PCB,即可判断出△AEF∽△BPC.
②过点C作CG⊥AB于G,设BG=a,由勾股定理可求出AB的长,再利用已知条件可求出FC和AF的长,进而可证明FC=2AF;
(2)首先根据AM∥BC,可得$\frac{AM}{BD}=\frac{AP}{BP}$,再根据AM=AP,可得BD=BP;然后判断出BC=BP,在Rt△ABC中,根据勾股定理,求出BP的值是多少,在△ACP中,由余弦定理,求出CP2的值是多少;最后在Rt△CMP中,根据勾股定理,求出PM的长是多少即可.
解答 (1)①证明:如图1, ,
,
∵AE⊥AB,
∴∠EAF+∠BAC=90°,
又∵∠PBC+∠BAC=90°,
∴∠EAF=∠PBC,
∵EP⊥CP,
∴∠CFP+∠FCP=90°,
又∵∠PCB+∠FCP=90°,
∴∠CFP=∠PCB,
∵∠EFA=∠CFP,
∴∠EFA=∠PCB,
在△AEF和△BPC中,
$\left\{\begin{array}{l}{∠EAF=∠PBC}\\{∠EFA=∠PCB}\end{array}\right.$,
∴△AEF∽△BPC;
②证明:如图2, 过点C作CG⊥AB于G,设BG=a,
过点C作CG⊥AB于G,设BG=a,
∵tan∠B=$\frac{AC}{BC}$=2,
∴CG=2a,
在Rt△BGC中,BC2=BG2+GC2,
∴BC=$\sqrt{5}$a,AC=2$\sqrt{5}$a,
在Rt△ABC中,AB2=AC2+BC2,
∴AB=5a,
∵$\frac{AP}{BP}$=$\frac{2}{3}$,
∴AP=2a,PG=2a,PB=3a,
∴PG=CG,
∴∠CPG=∠APE=∠E=45°,
∴AE=AP=2a,
由(1)得$\frac{AF}{BC}=\frac{AE}{BP}=\frac{2}{3}$,
∴AF=$\frac{2\sqrt{5}}{3}$a,CF=$\frac{4\sqrt{5}}{3}$a,
∴FC=2AF;
(2)解:如图3,MP和CB的延长线交于点D, ,
,
∵AM∥BC,
∴$\frac{AM}{BD}=\frac{AP}{BP}$,
∵AM=AP,
∴BD=BP,
∴∠BDP=∠BPD,
∵MP⊥CP,
∴∠BDP+∠BCP=90°,
又∵∠BPD+∠BPC=90°,
∴∠BCP=∠BPC,
∴BC=BP,
设BC=BP=x,
则(x+2)2=x2+42,
解得x=3,
∴AB=AP+BP=2+3=5,
∴cos∠CAP=$\frac{AC}{AB}$=$\frac{4}{5}$,
在△ACP中,由余弦定理,可得,
CP2=AP2+AC2-2AP•AC•cos∠CAP,
=22+42-2×2×4×$\frac{4}{5}$,
=7.2,
∵AC⊥BC,AM∥AC,
∴AM⊥AC,
∴CM2=AC2+AM2=42+22=16+4=20,
在Rt△CMP中,
∵PM2=CM2-CP2=20-7.2=12.8,
∴PM=$\sqrt{12.8}=\frac{8\sqrt{5}}{5}$.
点评 本题考查了相似形的综合题,用到的知识点有相似三角形的判定和性质、勾股定理的运用、等腰直角三角形的判定和性质、余弦定理的运用,锐角三角函数的定义,题目的综合性较强,难度较大,对学生的计算能力要求很高,是一道不错的中考压轴题.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
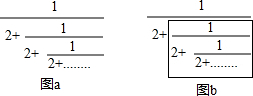 观察图a所示算式,该算式由无数层分数线及相同的加数2循环嵌套而成,由图b我们发现,因为有无数层分数线嵌套,因此方框内的部分与整个算式相同,我们假设算式的结果为x,那么就可以将该算式转化成$\frac{1}{2+x}$,从而得到方程$\frac{1}{2+x}$=x.求解出该算式的结果
观察图a所示算式,该算式由无数层分数线及相同的加数2循环嵌套而成,由图b我们发现,因为有无数层分数线嵌套,因此方框内的部分与整个算式相同,我们假设算式的结果为x,那么就可以将该算式转化成$\frac{1}{2+x}$,从而得到方程$\frac{1}{2+x}$=x.求解出该算式的结果查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com