
在同一直角坐标系中,画出下列函数的图象:
(1)y=x2+1;(2)y=x2-1;(3)y=-x2+1;(4)y=-2x2-1并从解析式、函数对应值、图象三个方面对比,说出解析式中二次项系数a对抛物线形状有什么影响?常数c对抛物线的位置有什么影响?
|
解:(1)列表:
描点、连线如下图.
(2)抛物线y=ax2+c的顶点是(0,c),对称轴是y轴,由抛物线y=x2+1,y=x2-1开口向上,可知当a>0时,抛物线顶点在y轴上,开口向上; 由抛物线y=-x2+1,y=-2x2-1开口向下,可知当a<0时,抛物线顶点在y轴上,开口向下. 由图象可知,抛物线y=x2+1,y=x2-1,y=-x2+1形状相同,位置不同. 当|a|相同时,抛物线形状相同; 当|a|变大时,抛物线开口变小,如上图所示; 当|a|变小时,抛物线开口变大. (3)由图象可知,抛物线y=x2+1,y=x2-1可由抛物线y=x2分别向上平移、向下平移1个单位而得到. 由此可知 当c>0时,将抛物线y=ax2向上平移c个单位,即可得到抛物线y=ax2+c; 当c<0时,将抛物线y=ax2向下平移|c|个单位,即可得到抛物线y=ax2+c. 思路点拨:(1)用描点法画二次函数y=ax2+c的图象时,应在对称轴上及左、右两侧对称的选取自变量x的值,然后计算出y的值.一般情况下,一定要包括顶点及另外的5至7个点即可,连接时要注意平滑,两边要延伸出去. (2)分a>0和a<0两种情况,分析a的取值对抛物线形状的影响. (3)分c>0和c<0两种情况,分析c的取值对抛物线位置的影响. 评注:在描图中,用平滑的曲线依次连接所描之点,靠近顶点部分特别要按规律描出曲线,不能出现以原点为顶点的角.画出图象,便于观察、分析得到函数性质. |


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
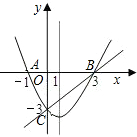 如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),一次函数的图象与抛物线交于B、C两点.
如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),一次函数的图象与抛物线交于B、C两点.查看答案和解析>>
科目:初中数学 来源: 题型:
 爱动脑筋的小明同学在买一双新的运动鞋时,发现了一些有趣现象,即鞋子的号码与鞋子的长(cm)之间存在着某种联系,经过收集数据,得到下表:
爱动脑筋的小明同学在买一双新的运动鞋时,发现了一些有趣现象,即鞋子的号码与鞋子的长(cm)之间存在着某种联系,经过收集数据,得到下表:| 鞋长x(cm) | … | 22 | 23 | 24 | 25 | 26 | … |
| 码数y | … | 34 | 36 | 38 | 40 | 42 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com