
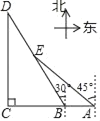
【题目】如图为某景区五个景点A,B,C,D,E的平面示意图,B,A在C的正东方向,D在C的正北方向,D,E在B的北偏西30°方向上,E在A的西北方向上,C,D相距1000![]() m,E在BD的中点处.
m,E在BD的中点处.
(1)求景点B,E之间的距离;
(2)求景点B,A之间的距离.(结果保留根号)
【答案】(1)1000(米);(2)500(![]() ﹣1)(米).
﹣1)(米).
【解析】
(1)根据已知条件得到∠C=90°,∠CBD=60°,∠CAE=45°,解直角三角形即可得到结论;
(2)过E作EF⊥AB与F,在Rt△AEF中,求得EF,在Rt△BEF中,求得BF,于是得到结论.
(1)由题意得,∠C=90°,∠CBD=60°,∠CAE=45°,
∵CD=1000![]() ,
,
∴BC=![]() =1000,
=1000,
∴BD=2BC=2000,
∵E在BD的中点处,
∴BE=![]() BD=1000(米);
BD=1000(米);
(2)过E作EF⊥AB与F,
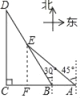
在Rt△AEF中,EF=AF=BEsin60°=1000×![]() =500
=500![]() ,
,
在Rt△BEF中,BF=BEcos60°=500,
∴AB=AF﹣BF=500(![]() ﹣1)(米).
﹣1)(米).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
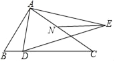
【题目】如图,在Rt△ABC中,∠BAC=90°,BC=5,AB=3,点D是线段BC上一动点,连接AD,以AD为边作△ADE∽△ABC,点N是AC的中点,连接NE,当线段NE最短时,线段CD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
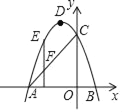
【题目】如图,在直角坐标系中,抛物线y=﹣(x+1)2+4与x轴交于点A、B,与y轴交于点C.
(1)写出抛物线顶点D的坐标 ;
(2)点D1是点D关于y轴的对称点,判断点D1是否在直线AC上,并说明理由;
(3)若点E是抛物线上的点,且在直线AC的上方,过点E作EF⊥x轴交线段AC于点F,求线段EF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
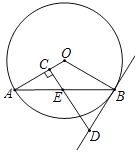
【题目】如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
(1)求证:BD是⊙O的切线;
(2)若AB=12,DB=5,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程![]() 有两个实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,一元二次方程
有两个实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,一元二次方程![]() 的两个根是2和4,则方程
的两个根是2和4,则方程![]() 就是“倍根方程”.
就是“倍根方程”.
(1)若一元二次方程![]() 是“倍根方程”,则c ;
是“倍根方程”,则c ;
(2)若![]() 是“倍根方程”,求代数式
是“倍根方程”,求代数式![]() 的值;
的值;
(3)若方程![]() 是倍根方程,且不同的两点M(k+1,5),N(3-k,5)都在抛物线
是倍根方程,且不同的两点M(k+1,5),N(3-k,5)都在抛物线![]() 上,求一元二次方程
上,求一元二次方程![]() 的根.
的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋中有4个完全相同的小球,把它们分别标上数字﹣1,0,1,2,随机的摸出一个小球记录数字然后放回,在随机的摸出一个小球记录数字.求下列事件的概率:
(1)两次都是正数的概率P(A);
(2)两次的数字和等于0的概率P(B).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王叔叔家是养猪专业户,他们养的藏香猪和土黑猪一直很受市民欢迎.小王今年10月份开店卖猪肉,已知藏香猪肉售价每斤![]() 元,土黑猪肉售价每斤
元,土黑猪肉售价每斤![]() 元,每天固定从叔叔家进货两种猪肉共
元,每天固定从叔叔家进货两种猪肉共![]() 斤并且能全部售完.
斤并且能全部售完.
(1)若每天销售总额不低于![]() 元,则每天至少销售藏香猪肉多少斤?
元,则每天至少销售藏香猪肉多少斤?
(2)小王发现10月份每天上午就能将猪肉全部售完,而且消费者对猪肉的评价很高.于是小王决定调整猪肉价格,并增加进货量,且能将猪肉全部销售完.他将藏香猪肉的价格上涨![]() ,土黑猪肉的价格下调
,土黑猪肉的价格下调![]() ,销量与(1)中每天获得最低销售总额时的销量相比,藏香猪肉销量下降了
,销量与(1)中每天获得最低销售总额时的销量相比,藏香猪肉销量下降了![]() ,土黑猪肉销量是原来的
,土黑猪肉销量是原来的![]() 倍,结果每天的销售总额比(1)中每天获得的最低销售总额还多了
倍,结果每天的销售总额比(1)中每天获得的最低销售总额还多了![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )

A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学报名参加学校运动会,有以下4个项目可供选择:
径赛项目:100m,200m,![]() 分别用
分别用![]() 、
、![]() 、
、![]() 表示
表示![]() ;
;
田赛项目:立定跳远![]() 用B表示
用B表示![]() .
.
![]() 小明从4个项目中任选一个,恰好是径赛项目的概率为______;
小明从4个项目中任选一个,恰好是径赛项目的概率为______;
![]() 小明从4个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
小明从4个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com