
【题目】如图,点D、E分别是等边三角形ABC的边BC、AC上的点,连接AD、BE交于点O,且△ABD≌△BCE.
(1)若AB=3,AE=2,则BD= ;
(2)若∠CBE=15°,则∠AOE= ;
(3)若∠BAD=a,猜想∠AOE的度数,并说明理由.

【答案】(1)BD=1;(2)60°;(3)∠AOE =60°.
【解析】
(1)根据等边三角形的性质求出AC,得到EC,根据全等三角形的性质解答;
(2)根据全等三角形的性质得到∠BAD=∠CBE=15°,根据三角形的外角性质计算即可;
(3)仿照(2)的作法解答.
解:(1)∵△ABC是等边三角形,
∴AC=AB=3,
∴EC=AC-AE=1,
∵△ABD≌△BCE,
∴BD=EC=1,
故答案为:1;
(2)∵△ABD≌△BCE,
∴∠BAD=∠CBE=15°,
∵∠CBE=15°,
∴∠ABO=45°,
∴∠AOE=∠BAD+∠ABO=60°,
故答案为:60°;
(3)由(2)得,∠BAD=∠CBE,
∵∠ABO+∠CBE=60°,
∴∠AOE=∠BAD+∠ABO=60°.


科目:初中数学 来源: 题型:
【题目】我市大力发展绿色交通,构建公共绿色交通体系,“共享单车”的投入使用给人们的出行带来便利.小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如图统计图,请根据图中信息,解答下列问题:
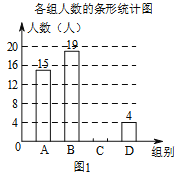
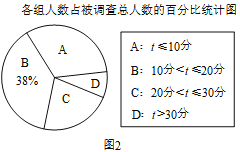
(1)这次被调查的总人数是______;
(2)补全条形统计图;
(3)在扇形统计图中,求表示A组(t≤10分)的扇形圆心角的度数;
(4)如果骑共享单车的平均速度为12km/h,请估算,在租用共享单车的市民中,骑车路程不超过6km的人数所占的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知反比例函数![]() 的图象的一支位于第一象限.
的图象的一支位于第一象限.
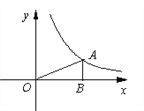
(1)该函数图象的另一分支位于第_____象限,m的取值范围是____________;
(2)已知点A在反比例函数图象上,AB⊥x轴于点B,△AOB的面积为3,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
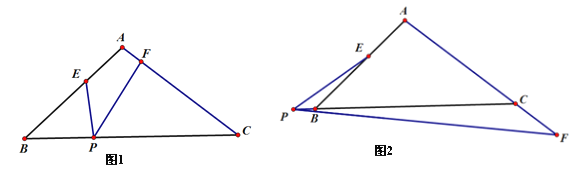
【题目】(1)如图1,△ABC中,∠BAC=100°,AB=AC,P为BC边上任意一点.若点E、F分别在AB、AC上,且∠EPF=40°,求证:△BPE∽△CFP;
(2)如图2,点P在边CB的延长线上,点E在边AB上,点F在边AC的延长线上,仍有∠EPF=40°,探索PB·PC与BE·CF有怎样的关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
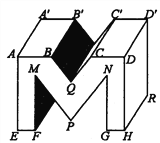
【题目】如图所示,在书写艺术字时,常常运用画“平行线段”这种基本作图方法,此图是在书写字“M”:
(1)请从正面,上面,右侧三个不同方向上各找出一组平行线段,并用字母表示出来;
(2)EF与A′B′有何位置关系?CC′与DH有何位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com