
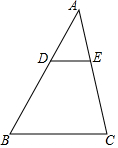
 如图,D、E分别是△ABC的边AB、AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )
如图,D、E分别是△ABC的边AB、AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )| A. | 4 | B. | 8 | C. | $\frac{21}{2}$ | D. | $\frac{25}{2}$ |
分析 先判断△ADE∽△ABC,再根据相似三角形的面积之比=相似比的平方即可得到结论.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}=\frac{DE}{BC}$,
∵AD=2,DB=3,
∴$\frac{AD}{AB}=\frac{DE}{BC}=\frac{2}{5}$,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}=(\frac{DE}{BC})^{2}=\frac{4}{25}$,
∵△ADE的面积是2,
∴△ABC的面积是12.5,
∴四边形BCED的面积是12.5-2=10.5,
故选C
点评 本题考查了相似三角形的判定和性质,注意:相似三角形的面积之比=相似比的平方.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
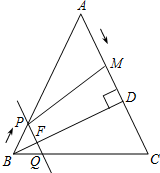 如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/秒;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/秒,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).
如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/秒;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/秒,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
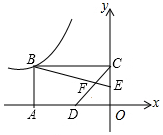 如图,双曲线y=-$\frac{42}{x}$的图象经过矩形OABC的顶点B,两边OA,OC在坐标轴上,且OD=$\frac{1}{3}$OA,E为OC的中点,BE与CD交于点F,则四边形EFDO的面积为$\frac{11}{2}$.
如图,双曲线y=-$\frac{42}{x}$的图象经过矩形OABC的顶点B,两边OA,OC在坐标轴上,且OD=$\frac{1}{3}$OA,E为OC的中点,BE与CD交于点F,则四边形EFDO的面积为$\frac{11}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
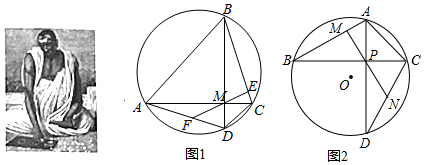
| 婆罗摩笈多是一位印度数学家与天文学家,书写了两部关于数学与天文的书籍,他的一些数学成就在世界数学史上有较高的地位,他的负数及加减法运算仅晚于中国九章算术而他的负数乘除法法则在全世界都是领先的,他还提出了著名的婆罗摩笈多定理,该定理的内容及证明如下: 已知:如图,四边形ABCD内接与圆O对角线AC⊥BD于点M,ME⊥BC于点E,延长EM交CD于F,求证:MF=DF 证明∵AC⊥BD,ME⊥BC ∴∠CBD=∠CME ∵∠CBD=∠CAD,∠CME=∠AMF ∴∠CAD=∠AMF ∴AF=MF ∵∠AMD=90°,同时∠MAD+∠MDA=90° ∴∠FMD=∠FDM ∴MF=DF,即F是AD中点. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
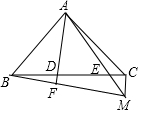 已知:在△ABC中,AB=AC,AB⊥AC,D、E在BC上,且∠ADC=∠BAE.
已知:在△ABC中,AB=AC,AB⊥AC,D、E在BC上,且∠ADC=∠BAE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com