随着人们对健康认知度的提高,人们对食品的健康要求也越来越高,我市对食品安全检查的力度也越来越强.某一奶制品企业经销某种牛奶,已知每箱牛奶的成本为40元,其每个月的销量y(万箱)与销售单价x(元)的关系如下表所示(x为5的倍数,且x≤80元).
售价x
(元) |
… |
60 |
65 |
70 |
75 |
80 |
月销量y
(万箱) |
… |
6 |
5.5 |
5 |
4.5 |
4 |
又已知该企业每月销售该种牛奶的总开支z(万元)(不含牛奶成本)与销量y(万箱)存在函数关系:z=10y+42.
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求出月销量y与售价x之间的函数关系式;
(2)当售价定为何值时,月销售利润最大?且最大是多少?
(3)到今年2月底止,该企业都在获得最大利润的基础上进行销售,从今年3月份开始,该企业为满足人们需要,积极响应市里号召,停止生产该种牛奶准备加工生产一种高优质牛奶,于是采取了一系列优化措施,其中添置生产处理设备共250万元,并增加安全技术人员50名,这样每月的总开支(不含牛奶成本)将比2月份增加5万元,而一箱牛奶的成本比原来增加了25%,但该企业为了促销新品种牛奶,3月份每箱牛奶的售价却比2月份下降了25%,3月的销量比2月增加了40%,到了4月份取消促销活动,每箱牛奶的价格在3月份的基础上增加了n%,销量在3月份的基础上增加了0.25n%,以这样的销售持续到5月底,则从2月到5月共获利润295万元,试估计n的整数值.(32
2=1024,33
2=1089,34
2=1156)



 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案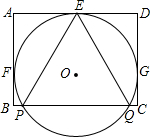 如图,⊙O与矩形ABCD的AD、AB、CD的三边分别相切于E、F、G三点,边BC与⊙O交于P、Q两点,若AD=4,AB=3,则sin∠PEQ的值为( )
如图,⊙O与矩形ABCD的AD、AB、CD的三边分别相切于E、F、G三点,边BC与⊙O交于P、Q两点,若AD=4,AB=3,则sin∠PEQ的值为( )