
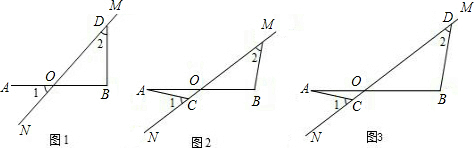
��ͼ1��ͼ4�У���ƽ����AB��CD��ľ����Ϊ6����MΪAB��һ���㣮

˼����
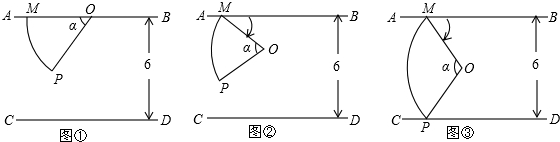
��ͼ1��Բ��Ϊ0�İ�Բ��ֽƬ��AB��CD֮�䣨����AB��CD������ֱ��MN��AB�ϣ�MN=8����PΪ��Բ��һ�㣬���MOP=����
����=�� ����ʱ����P��CD�ľ�����С����СֵΪ�� ����
̽��һ��
��ͼ1�Ļ����ϣ��Ե�MΪ��ת���ģ���AB��CD ֮��˳ʱ����ת�ð�Բ��ֽƬ��ֱ��������ת��Ϊֹ����ͼ2���õ������ת�ǡ�BMO=�� ���ȣ���ʱ��N��CD�ľ������� ����
̽������
����ͼ1�е�����ֽƬNOP������Ԧ���Ҫ�������ʹ����ֽƬMOP�Ƶ�M��AB��CD֮��˳ʱ����ת��
��1����ͼ3������=60��ʱ��������ת�����У���P��CD����С���룬����ָ����ת�ǡ�BMO�����ֵ��
��2����ͼ4��������ֽƬMOP��ת�����У�Ҫ��֤��P������ֱ��CD�ϣ���ȷ���������ֵ��
˼����90��2��̽��һ����BMO=30�ȣ���ʱ��N��CD�ľ����� 2̽��������1��90�㣨2��120��
����������MN=8��
��OP=4��
���P��CD�ľ�����СֵΪ��6��4=2��
�ʴ�Ϊ��90��2�� ������������������������2��
̽��һ��
���Ե�MΪ��ת���ģ���AB��CD ֮��˳ʱ����ת�ð�Բ��ֽƬ��ֱ��������ת��Ϊֹ��
��MN=8��MO=4��ON=4��
���N��CD�ľ�����6��4=2
��õ������ת�ǡ�BMO=30�ȣ���ʱ��N��CD�ľ����� 2������������������������6��
̽����
��1������֪�ó�M��P�ľ���Ϊ4��
��PM��ABʱ����P��AB����������4���Ӷ���P��CD����С����Ϊ6��4=2��
������MOP��AB��CD֮����ת��������תʱ����MP��AB���У�
��ʱ��ת�����BMO�����ֵΪ90�㣻 ������������������������ 9��
��2����ͼ����̽��һ��֪����P�ǻ�MP��CD������ʱ���������OP��CD����ʱ�ӳ�PO��AB�ڵ�H�������ֵΪ��OMH+��OHM=30��+90��=120�㡣
����������������������12��
������ƽ����֮�䴹�߶���̣��Լ����ߵ����ʶ�����ֱ�ӵó��𰸣�
̽��һ��������MN=8��MO=4��OY=4���ó�UO=2�����ɵó��õ������ת�ǡ�BMO=30�ȣ���ʱ��N��CD�ľ����� 2��
̽��������1������֪�ó�M��P�ľ���Ϊ4��PM��ABʱ����MP��AB����������4���Ӷ���P��CD����С����Ϊ6��4=2�����ɵó���BMO�����ֵ��
��2���ֱ���������ֵΪ��OMH+��OHM=30��+90���Լ���Сֵ��=2��MOH�����ɵó�����ȡֵ��Χ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| BD | AC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�


�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com