
【题目】如图,在等边三角形ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB交BC于点D,OE∥AC交BC于点E.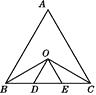
(1)试判断△ODE的形状,并说明你的理由;
(2)若BC=10,求△ODE的周长.
【答案】
(1)解:△ODE是等边三角形.理由如下:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°.
∴∠DOE=60°.
∴∠DOE=∠ODE=∠OED.
∴△ODE是等边三角形 。
(2)解:∵BO平分∠ABC,且∠ABC=60°,
∴∠OBD=30°.
∴∠BOD=∠ODE-∠OBD=60°-30°=30°.
∴∠OBD=∠BOD.
∴BD=OD.
同理可得:CE=OE.
∴△ODE的周长=OD+DE+OE=BD+DE+CE=BC=10
【解析】(1)△ODE是等边三角形.理由如下:根据等边三角形的性质得出∠ABC=∠ACB=60°,根据二直线平行,同位角相等得出∠ODE=∠ABC=60°,∠OED=∠ACB=60°,根据三角形的内角和得出∠DOE=60°,从而得出∠DOE=∠ODE=∠OED,根据三个内角都相等的三角形是等边三角形得出△ODE是等边三角形;
(2)根据角平分线的定义得出∠OBD=30°,根据三角形的外角定理得出∠BOD=∠ODE-∠OBD=60°-30°=30°,从而得出∠OBD=∠BOD,根据等角对等边得出BD=OD,同理可得:CE=OE,根据△ODE的周长=OD+DE+OE=BD+DE+CE=BC得出结论。


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=![]() x+m经过点A(﹣2,n),B(1,
x+m经过点A(﹣2,n),B(1, ![]() ),抛物线y=x2﹣2tx+t2﹣1与x轴相交于点C,D.
),抛物线y=x2﹣2tx+t2﹣1与x轴相交于点C,D.
(1)求点A的坐标;
(2)设点E的坐标为(![]() ,0),若点C,D都在线段OE上,求t的取值范围;
,0),若点C,D都在线段OE上,求t的取值范围;
(3)若该抛物线与线段AB有公共点,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左到右的变形是因式分解的是( )
A.(a+3)(a﹣3)=a2﹣9
B.x2+4x+10=(x+2)2+6
C.x2﹣6x+9=(x﹣3)2
D.x2﹣4+3x=(x﹣2)(x+2)+3x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解七年级男生体质健康情况,随机抽取若干名男生进行测试,测试结果分为优秀、良好、合格、不合格四个等级,统计整理数据并绘制图1、图2两幅不完整的统计图,请根据图中信息回答下列问题:

(1)本次接收随机抽样调查的男生人数为 人,扇形统计图中“良好”所对应的圆心角的度数为 ;
(2)补全条形统计图中“优秀”的空缺部分;
(3)若该校七年级共有男生480人,请估计全年级男生体质健康状况达到“良好”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是( )
A.y=(x﹣4)2﹣6
B.y=(x﹣4)2﹣2
C.y=(x﹣2)2﹣2
D.y=(x﹣1)2﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
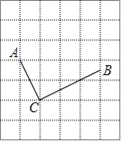
【题目】如图,在每个小正方形边长为1的网格中,点A,点C均落在格点上,点B为中点.
(Ⅰ)计算AB的长等于_____;
(Ⅱ)若点P,Q分别为线段BC,AC上的动点,且BP=CQ,请在如图所示的网格中,用无刻度的直尺,画出当PQ最短时,点P,Q的位置,并简要说明画图方法(不要求证明)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计,“五一”小长假期间,大连市共接待海内外游客825400余人次,数825100用科学记数法表示为( )
A.8251×102
B.825.1×103
C.82.51×104
D.8.251×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司要设计一块面积为10平方米的正方形广告牌,公司在设计广告时,必须知道这个正方形的边长.这个正方形的边长是多少?估计边长的值(结果精确到十分位).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com