
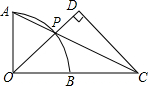
 如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OB=BC=1,则PD的长为( )
如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OB=BC=1,则PD的长为( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 过点O作OE⊥AP于点E,证△AOE∽△ACO得$\frac{AO}{AC}$=$\frac{AE}{AO}$,由OA=OB=BC=1得AC=$\sqrt{A{O}^{2}+O{C}^{2}}$=$\sqrt{5}$,从而得$\frac{1}{\sqrt{5}}$=$\frac{AE}{1}$,即AE=$\frac{\sqrt{5}}{5}$,由垂径定理得PE=AE=$\frac{\sqrt{5}}{5}$,再证△OPE∽△CPD得$\frac{PE}{PD}$=$\frac{OP}{CP}$,即$\frac{\frac{\sqrt{5}}{5}}{PD}$=$\frac{1}{\frac{3\sqrt{5}}{5}}$,从而得出答案.
解答 解:过点O作OE⊥AP于点E,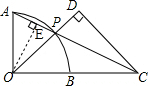
则∠AEO=∠AOC=90°,
∵∠OAE=∠CAO,
∴△AOE∽△ACO,
∴$\frac{AO}{AC}$=$\frac{AE}{AO}$,
∵OA=OB=BC=1,
∴AC=$\sqrt{A{O}^{2}+O{C}^{2}}$=$\sqrt{5}$,
∴$\frac{1}{\sqrt{5}}$=$\frac{AE}{1}$,得AE=$\frac{\sqrt{5}}{5}$,
∵OE⊥AP,
∴PE=AE=$\frac{\sqrt{5}}{5}$,
∴PC=AC-AP=$\frac{3\sqrt{5}}{5}$,
∵∠OEP=∠D=90°,∠OPE=∠CPD,
∴△OPE∽△CPD,
∴$\frac{PE}{PD}$=$\frac{OP}{CP}$,即$\frac{\frac{\sqrt{5}}{5}}{PD}$=$\frac{1}{\frac{3\sqrt{5}}{5}}$,
解得:PD=$\frac{3}{5}$,
故选:C.
点评 本题主要考查相似三角形的判定与性质、垂径定理、勾股定理等知识点,根据题意构建与直角边PD相关的相似三角形是解题的出发点也是关键.


科目:初中数学 来源:2017届吉林省九年级下学期第二次月考数学试卷(解析版) 题型:单选题
如图,在⊙O中,弦AC∥半径OB,∠BOC=40°,则∠OAB的度数为( )
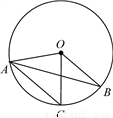
A. 25° B. 20° C. 60° D. 30°
查看答案和解析>>
科目:初中数学 来源:2017届辽宁省丹东市九年级第一次模拟考试数学试卷(解析版) 题型:判断题
甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在△ABC中,AB=$\sqrt{3}$,BC=4,∠ABC=60°,以AC为斜边作等腰Rt△ACD,连接BD,则BD的长度为$\frac{\sqrt{62}}{2}$.
在△ABC中,AB=$\sqrt{3}$,BC=4,∠ABC=60°,以AC为斜边作等腰Rt△ACD,连接BD,则BD的长度为$\frac{\sqrt{62}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
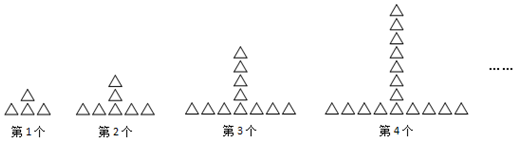
| A. | 46 | B. | 48 | C. | 50 | D. | 52 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com