
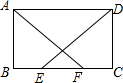
 如图,在?ABCD中,E、F为边BC上两点,且BE=CF,AF=DE.
如图,在?ABCD中,E、F为边BC上两点,且BE=CF,AF=DE.分析 (1)首先根据平行四边形的性质得到AB=CD,然后结合已知条件利用SSS判定两三角形全等即可;
(2)根据全等三角形的性质得到∠B=∠C=90°,从而判定矩形.
解答 解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,
∵BE=CF,
∴BF=CE,
在△ABF和△DCE中,
$\left\{\begin{array}{l}{AB=CD}\\{AF=DE}\\{BF=CE}\end{array}\right.$,
∴△ABF≌△DCE;
(2)四边形ABCD是矩形;
证明:∵△ABF≌△DCE,
∴∠B=∠C,
∵在平行四边形ABCD中,
∠B+∠C=180°,
∴∠B=∠C=90°,
∴四边形ABCD是矩形;
点评 本题考查了全等三角形的判定及矩形的判定的知识,解题的关键是了解有关的判定定理,难道不大.


科目:初中数学 来源: 题型:选择题
| A. | x≥3 | B. | 0≤x≤3 | C. | x≥0 | D. | x>3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
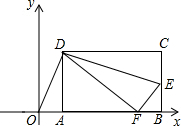 如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(3,4),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点C的坐标为(8,4)或(3$+2\sqrt{5}$,4)或($\frac{43}{6}$,4).
如图,矩形ABCD的顶点AB在x轴上,点D的坐标为(3,4),点E在边BC上,△CDE沿DE翻折后点C恰好落在x轴上点F处,若△ODF为等腰三角形,点C的坐标为(8,4)或(3$+2\sqrt{5}$,4)或($\frac{43}{6}$,4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
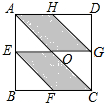 如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,E,F,G,H分别是AB,BC,CD,AD的中点,阴影部分EOCF,AOGH都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
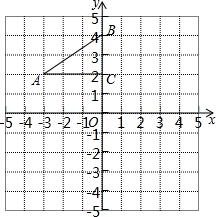 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
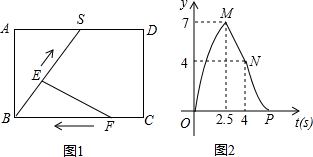
| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
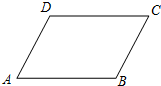 如图,已知四边形ABCD中,AB∥CD,若不添加任何辅助线,请添加一个条件:
如图,已知四边形ABCD中,AB∥CD,若不添加任何辅助线,请添加一个条件:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com