
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
分析 (1)根据图表中的各数可得出y与x成一次函数关系,从而结合图表的数可得出y与x的关系式.
(2)根据想获得4000元的利润,列出方程求解即可;
(3)根据批发商获得的总利润w(元)=售量×每件利润可表示出w与x之间的函数表达式,再利用二次函数的最值可得出利润最大值.
解答 解:
(1)设y与x的函数关系式为y=kx+b(k≠0),根据题意得
$\left\{\begin{array}{l}{50k+b=100}\\{60k+b=90}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=150}\end{array}\right.$.
故y与x的函数关系式为y=-x+150;
(2)根据题意得
(-x+150)(x-20)=4000,
解得x1=70,x2=100>90(不合题意,舍去).
故该批发商若想获得4000元的利润,应将售价定为70元;
(3)w与x的函数关系式为:
w=(-x+150)(x-20)
=-x2+170x-3000
=-(x-85)2+4225,
∵-1<0,
∴当x=85时,w值最大,w最大值是4225.
∴该产品每千克售价为85元时,批发商获得的利润w(元)最大,此时的最大利润为4225元.
点评 本题考查二次函数的应用,难度较大,解答本题的关键是根据题意列出方程,另外要注意掌握二次函数的最值的求法.


科目:初中数学 来源: 题型:选择题
| A. | 2(1-x)2=3.92 | B. | 3.92(1-x)2=2 | C. | 2(1+x)2=3.92 | D. | 3.92(1+x)2=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
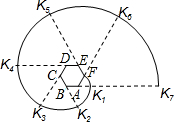 如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1,弧K1K2,弧K2K3,弧K3K4,弧K4K5,弧K5K6,…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为L1,L2,L3,L4,L5,L6,….当AB=1时,L2016等于( )
如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1,弧K1K2,弧K2K3,弧K3K4,弧K4K5,弧K5K6,…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为L1,L2,L3,L4,L5,L6,….当AB=1时,L2016等于( )| A. | $\frac{2016π}{2}$ | B. | $\frac{2016π}{3}$ | C. | $\frac{2016π}{4}$ | D. | $\frac{2016π}{6}$. |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com