
【题目】计算下面各题
①﹣40﹣28﹣(﹣19)+(﹣24)
②(﹣1![]() )×(﹣10)÷|﹣0.7|
)×(﹣10)÷|﹣0.7|
③﹣32﹣4×(﹣3)+15÷(﹣3)
④3x2﹣[7x﹣(4x﹣3)﹣2x2]
⑤5(a2b﹣3ab2)﹣2(a2b﹣7ab2)
【答案】①﹣73;②20;③﹣2;④5x2﹣3x﹣3;⑤3a2b﹣ab2.
【解析】
①将减法转化为加法,再根据法则计算即可;
②将除法转化为乘法,再计算乘法即可;
③根据有理数的混合运算顺序和运算法则计算即可;
④先去括号,再合并同类项即可;
⑤先去括号,再合并同类项即可.
①原式=﹣40﹣28+19﹣24
=﹣40﹣28﹣24+19
=﹣92+19
=﹣73;
②原式![]() (﹣10)
(﹣10)![]() =20;
=20;
③原式=﹣9+12+(﹣5)
=3+(﹣5)
=﹣2;
④原式=3x2﹣7x+(4x﹣3)+2x2
=3x2﹣7x+4x﹣3+2x2
=5x2﹣3x﹣3;
⑤原式=5a2b﹣15ab2﹣2a2b+14ab2=3a2b﹣ab2.


科目:初中数学 来源: 题型:
【题目】现有边长相等的正三角形、正方形、正六进形、正八边形形状的地砖,如果选择其中的两钟铺满平整的地面,那么选择的两种地砖形状不能是( )
A. 正三角形与正方形 B. 正三角形与正六边形
C. 正方形与正六边形 D. 正方形与正八边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已如点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2019个单位长度没有弹性的细线(线的相细忽略不计)的一端固定在A处,并按![]() 的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是__________.
的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB⊥BE于点B,DE⊥BE于点E.
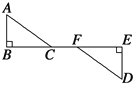
(1)若∠A=∠D,AB=DE,则△ABC与△DEF全等的理由是____;
(2)若∠A=∠D,BC=EF,则△ABC与△DEF全等的理由是_________;
(3)若AB=DE,BC=EF,则△ABC与△DEF全等的理由是_______;
(4)若AB=DE,AC=DF,则△ABC与△DEF全等的理由是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的个数是( )
①2a2﹣a2=a2;
② ![]() +
+ ![]() =2
=2 ![]() ;
;
③(π﹣3.14)0× ![]() =0;
=0;
④a2÷a× ![]() =a2;
=a2;
⑤sin30°+cos60°= ![]() ;
;
⑥精确到万位6295382≈6.30×106 .
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写推理理由:
已知:如图,D,F,E分别是BC,AC,AB上的点,DF∥AB,DE∥AC,

试说明∠EDF=∠A.
解:∵DF∥AB(已知),
∴∠A+∠AFD=180°(____________________).
∵DE∥AC(已知),
∴∠AFD+∠EDF=180°(____________________).
∴∠A=∠EDF(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=2,则AC的长为( )
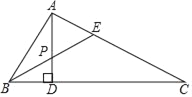
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.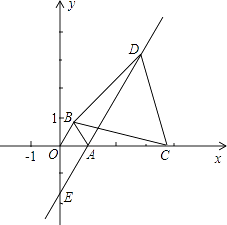
(1)如图,当C点在x轴上运动时,设AC=x,请用x表示线段AD的长;
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,当点C坐标为多少时直线EF∥直线BO?这时OF和直线BO的位置关系如何?请给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com