
【题目】四边形![]() 是正方形,
是正方形,![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 、
、![]() 是直线
是直线![]() 上两动点,且
上两动点,且![]() ,
,![]() 所在直线与对角线
所在直线与对角线![]() 所在直线交于点
所在直线交于点![]() ,连接
,连接![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.
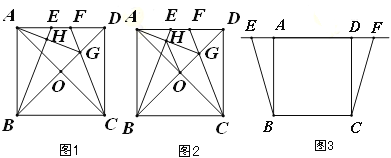
(1)如图1,当点![]() 、
、![]() 在线段
在线段![]() 上时,
上时,
①求证:![]() ;
;
②猜想![]() 与
与![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)如图2,在(1)条件下,连接![]() ,试说明
,试说明![]() 平分
平分![]() ;
;
(3)当点![]() 、
、![]() 运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出
运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出![]() 的度数.
的度数.
【答案】(1)证明见解析;(2)证明见解析;(3)图见解析;45°.
【解析】
试题分析:(1)①根据正方形的性质可证DA=DC,∠ADB=∠CDB=45°根据SAS可证△ADG≌△CDG,根据全等三角形的性质可证∠DAG=∠DCG;
②根据正方形的性质可证AB=DC,∠BAD=∠CDA=90°,根据SAS可证△ABE≌△DCF,根据全等三角形的性质可证∠ABE=∠DCF,根据∠DAG+∠BAG=90°可证∠AHB=∠ABE+∠BAG=90°,所以可证AG⊥BE;
(2) 过点O作OM⊥BE于点M,ON⊥AG于点N,则四边形OMHN为矩形,根据矩形的性质可得:∠AON=∠BOM,∠OAN=∠OBM,根据ASA可证△AON≌△BOM,根据全等三角形的性质可证OM=ON,所以可证矩形OMHN为正方形,根据正方形的性质可证HO平分∠BHG;
(3)图见解析;根据正方形的性质可证AG⊥BE,过点O作OM⊥BE于点M,ON⊥AG于点N,则可证△AON≌△BOM,根据全等三角形的性质可证OMHN为正方形,所以HO平分∠BHG,所以可证∠BHO=45°.
试题解析:(1)①∵四边形ABCD为正方形,
∴DA=DC,∠ADB=∠CDB=45°,
在△ADG和△CDG中
 ,
,
∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCG;
②AG⊥BE.理由如下:
∵四边形ABCD为正方形,
∴AB=DC,∠BAD=∠CDA=90°,
在△ABE和△DCF中
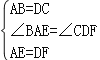 ,
,
∴△ABE≌△DCF(SAS),
∴∠ABE=∠DCF,
∵∠DAG=∠DCG,
∴∠DAG=∠BAE,
∵∠DAG+∠BAG=90°,
∴∠ABE+∠BAG=90°,
∴∠AHB=90°,
∴AG⊥BE;
(2)由(1)可知AG⊥BE.
如答图1所示,过点O作OM⊥BE于点M,ON⊥AG于点N,则四边形OMHN为矩形.
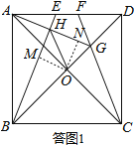
∴∠MON=90°,又∵OA⊥OB,
∴∠AON=∠BOM.
∵∠AON+∠OAN=90°,∠BOM+∠OBM=90°,
∴∠OAN=∠OBM.
在△AON与△BOM中,
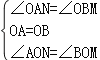
∴△AON≌△BOM(ASA).
∴OM=ON,
∴矩形OMHN为正方形,
∴HO平分∠BHG;
(3)将图形补充完整,如答图2示,∠BHO=45°.
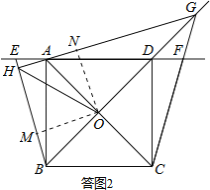
与(1)同理,可以证明AG⊥BE.
过点O作OM⊥BE于点M,ON⊥AG于点N,
与(2)同理,可以证明△AON≌△BOM,
可得OMHN为正方形,
∴HO平分∠BHG,
∴∠BHO=45°.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】下列说法错误的是( ).
A. 对角线互相平分的四边形为平行四边形
B. 两组对角分别相等的四边形为平行四边形
C. 一组对边平行且相等的四边形是平行四边形
D. 一组对边平行,另一组对边相等的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
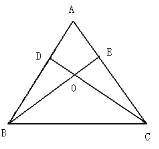
【题目】已知:如图,锐角△ABC的两条高BE、CD相交于点O,且OB=OC,
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少3000元.每天工作8小时,一个月工作25天.月工资底薪800元,另加计件工资.加工1件![]() 型服装计酬16元,加工1件
型服装计酬16元,加工1件![]() 型服装计酬12元.在工作中发现一名熟练工加工1件
型服装计酬12元.在工作中发现一名熟练工加工1件![]() 型服装和2件
型服装和2件![]() 型服装需4小时,加工3件
型服装需4小时,加工3件![]() 型服装和1件
型服装和1件![]() 型服装需7小时.(工人月工资=底薪+计件工资)
型服装需7小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件![]() 型服装和1件
型服装和1件![]() 型服装各需要多少小时?
型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工![]() ,
,![]() 两种型号的服装,且加工
两种型号的服装,且加工![]() 型服装数量不少于
型服装数量不少于![]() 型服装的一半”.设一名熟练工人每月加工
型服装的一半”.设一名熟练工人每月加工![]() 型服装
型服装![]() 件,工资总额为
件,工资总额为![]() 元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形属于因式分解的是( )
A. 4x+x=5xB. (x+2)2=x2+4x+4
C. x2+x+1=x(x+1)+1D. x2﹣3x=x(x﹣3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com